
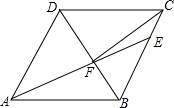
 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2$\sqrt{3}$;③tan∠DCF=$\frac{3\sqrt{3}}{7}$;④△ABF的面积为$\frac{12}{5}$$\sqrt{3}$.其中一定成立的是①②③(把所有正确结论的序号都填在横线上).
如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2$\sqrt{3}$;③tan∠DCF=$\frac{3\sqrt{3}}{7}$;④△ABF的面积为$\frac{12}{5}$$\sqrt{3}$.其中一定成立的是①②③(把所有正确结论的序号都填在横线上). 分析 利用SAS证明△ABF与△CBF全等,得出①正确,根据含30°角的直角三角形的性质得出点E到AB的距离是2$\sqrt{3}$,得出②正确,同时得出;△ABF的面积为$\frac{18\sqrt{3}}{5}$得出④错误,得出tan∠DCF=$\frac{3\sqrt{3}}{7}$,得出③正确.
解答 解:∵菱形ABCD,
∴AB=BC=6,
∵∠DAB=60°,
∴AB=AD=DB,∠ABD=∠DBC=60°,
在△ABF与△CBF中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABF=∠FBC}\\{BF=BF}\end{array}\right.$,
∴△ABF≌△CBF(SAS),
∴①正确;
过点E作EG⊥AB,过点F作MH⊥CD,MH⊥AB,如图: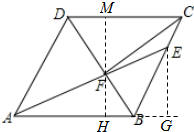
∵CE=2,BC=6,∠ABC=120°,
∴BE=6-2=4,
∵EG⊥AB,
∴EG=$2\sqrt{3}$,
∴点E到AB的距离是2$\sqrt{3}$,
故②正确;
∵BE=4,EC=2,
∴S△BFE:S△FEC=4:2=2:1,
∴S△ABF:S△FBE=3:2,
∴△ABF的面积为=$\frac{3}{5}{S}_{△ABE}=\frac{3}{5}×\frac{1}{2}×6×2\sqrt{3}=\frac{18\sqrt{3}}{5}$,
故④错误;
∵${S}_{△ADB}=\frac{1}{2}×6×3\sqrt{3}=9\sqrt{3}$,
∴${S}_{△DFC}={S}_{△ADB}-{S}_{△ABF}=9\sqrt{3}-\frac{18\sqrt{3}}{5}$=$\frac{27\sqrt{3}}{5}$,
∵${S}_{△DFC}=\frac{1}{2}×6×FM=\frac{27\sqrt{3}}{5}$,
∴FM=$\frac{9\sqrt{3}}{5}$,
∴DM=$\frac{MF}{\sqrt{3}}=\frac{\frac{9\sqrt{3}}{5}}{\sqrt{3}}=\frac{9}{5}$,
∴CM=DC-DM=6-$\frac{9}{5}=\frac{21}{5}$,
∴tan∠DCF=$\frac{MF}{CM}=\frac{\frac{9\sqrt{3}}{5}}{\frac{21}{5}}=\frac{3\sqrt{3}}{7}$,
故③正确;
故答案为:①②③
点评 此题考查了四边形综合题,关键是根据菱形的性质、等边三角形的判定与性质以及全等三角形的判定与性质分析.此题难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
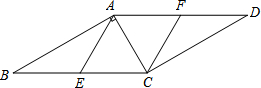 如图,已知点E,F分别是?ABCD的边BC,AD上的中点,且∠BAC=90°.
如图,已知点E,F分别是?ABCD的边BC,AD上的中点,且∠BAC=90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
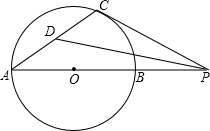 已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )
已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )| A. | 30° | B. | 20° | C. | 45° | D. | 25° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x+2)2+3 | B. | y=(x-2)2+3 | C. | y=(x+2)2-3 | D. | y=(x-2)2-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com