
����Ŀ��Ϊ�����л���ͳ�Ļ���ijУ��չ��˫����������Ļ����Уͯ�������ȡ����ѧ�������ĸ����![]() ��ʾ����ϲ������
��ʾ����ϲ������![]() ��ʾ��ϲ������
��ʾ��ϲ������![]() ��ʾ��һ������
��ʾ��һ������![]() ��ʾ����ϲ�������������ǶԺ����ϲ���������������Ƴ�����������������ͳ��ͼ������ͼ���ṩ����Ϣ������������⣺
��ʾ����ϲ�������������ǶԺ����ϲ���������������Ƴ�����������������ͳ��ͼ������ͼ���ṩ����Ϣ������������⣺
��1����ι���ȡ_________��ѧ������ͳ�Ƶ��飬����ͳ��ͼ�У�![]() ������Ӧ������Բ�ĽǵĴ�СΪ__________
������Ӧ������Բ�ĽǵĴ�СΪ__________
��2��������ͳ��ͼ��������
��3����У����1500��ѧ�������Ƹ�У��ʾ��ϲ������![]() ���ѧ����Լ�ж����ˣ�
���ѧ����Լ�ж����ˣ�
����ѧ����������ͳ��ͼ����ѧ����������ͳ��ͼ


���𰸡���1��50��72��.��1������������3��690��.
��������
(1)����C��ѧ���������Լ���ռ�ı�������ó�ȡ��ѧ����������360�ȳ���D��ѧ����ռ�ı���������ô𰸣�
(2)�����A���ѧ������Ȼ��ȫͳ��ͼ���ɣ�
(3)��1500����B��ѧ����ռ�ı������ɵ�.
(1)��ι���ȡ��12��24%=50��ѧ������ͳ�Ƶ��飬
![]() ������Ӧ������Բ�ĽǵĴ�СΪ360���
������Ӧ������Բ�ĽǵĴ�СΪ360���![]() =72����
=72����
�ʴ�Ϊ��50��72����
(2)A��ѧ������50-23-12-10=5��
��ȫͳ��ͼ��ͼ��ʾ��
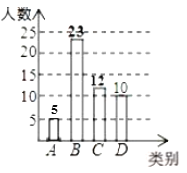
(3)![]() (��)��
(��)��
�𣺹��Ƹ�У��ʾ��ϲ������![]() ���ѧ����Լ��690��.
���ѧ����Լ��690��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼΪ���κ���y=ax2+bx+c��a��0����ͼ��������˵������a��0 ��2a+b=0 ��a+b+c��0 �ܵ���1��x��3ʱ��y��0��������ȷ�ĸ���Ϊ��������

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺����һ���߶�Ϊ�Խ����������Σ���Ƹ�������Ϊ�����߶ε����Խ����������������磬ͼ����������ABCD��Ϊ�߶�BD�����Խ���������������ͼ�ڣ��ڡ�ABC�У���ABC=90�㣬AB=3cm��BC=4cm����P�ӵ�C������������CA��AB��5cm/s���ٶ��˶�������P���B���غ�ʱ�����߶�PB�����Խ����������������P���˶�ʱ��Ϊt��s�����߶�PB�����Խ����������������ΪS��cm2����
��1����ͼ�ۣ��������ߵ�С�������������߶�AB�����Խ�������������
��2�����߶�PB�����Խ�����������������ͬʱ���ڡ�ABC�ı���ʱ����t��ֵ��
��3������P������CA��AB�˶�ʱ����S��t֮��ĺ�����ϵʽ��
��4���������˶������У����߶�PB�����Խ�����������������һ���������ڡ�A��ƽ������ʱ��ֱ��д��t��ֵ��



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A��0��2![]() ��������B��C��ԭ��Oͬʱ�������ֱ���ÿ��1����λ��ÿ��2����λ���ȵ��ٶ���x���������˶����Ե�AΪԲ�ģ�OB�ij�Ϊ�뾶��Բ����BCΪһ�ߣ���x���Ϸ����ȱ���BCD.���˶���ʱ��Ϊt�룬����A����BCD�ı�BD����ֱ������ʱ��t��ֵΪ�� ��
��������B��C��ԭ��Oͬʱ�������ֱ���ÿ��1����λ��ÿ��2����λ���ȵ��ٶ���x���������˶����Ե�AΪԲ�ģ�OB�ij�Ϊ�뾶��Բ����BCΪһ�ߣ���x���Ϸ����ȱ���BCD.���˶���ʱ��Ϊt�룬����A����BCD�ı�BD����ֱ������ʱ��t��ֵΪ�� ��

A. ![]() B.
B. ![]() C. 4
C. 4![]() ��6 D. 4
��6 D. 4![]() ��6
��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���E�ڶԽ���AC�ϣ�����EB��ED.
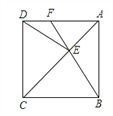
��1����֤����BCE�ա�DCE��
��2���ӳ�BE��AD�ڵ�F������DEB��140�����AFE�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ƻ�����A�ͺ�B�Ϳ����ʹ�200�ף����б꣬����һ��A�Ϳ����ʱȹ���һ��B�Ϳ���������40Ԫ�����ҹ���4��A�ͺ�6��B�Ϳ����ʹ���1820Ԫ��
��1������һ��A�Ϳ����ʺ�һ��B�Ϳ����ʸ������Ԫ��
��2��ѧУ����ʵ�������Ҫ���������ֿ������ܷ��ò��ܳ���40880Ԫ�����ҹ���A�Ϳ����ʵ��������ܳ���B�Ϳ����ʵ�![]() �����У���ι���A�ͺ�B�Ϳ����ʹ��м��ַ��������ַ������ܷ�����ͣ�
�����У���ι���A�ͺ�B�Ϳ����ʹ��м��ַ��������ַ������ܷ�����ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽��
��1����ͼ������֪������ABCD�ı߳�Ϊ4����M��N�ֱ��DZ�BC��CD�����㣬��BM=CN������AM��BN�����ڵ�P������AM��BN��λ�ù�ϵ����֤����Ľ��ۣ�
��2����ͼ������֪������ABCD�ı߳�Ϊ4����M��N�ֱ�ӵ�B��Cͬʱ����������ͬ���ٶ���BC��CD�������յ�C��D�˶�������AM��BN�����ڵ�P������APB�ܳ������ֵ��
������
��3����ͼ����ACΪ�߳�Ϊ2![]() ������ABCD�ĶԽ��ߣ���ABC=60�㣮��M��N�ֱ�ӵ�B��Cͬʱ����������ͬ���ٶ���BC��CA���յ�C��A�˶�������AM��BN�����ڵ�P������APB�ܳ������ֵ��
������ABCD�ĶԽ��ߣ���ABC=60�㣮��M��N�ֱ�ӵ�B��Cͬʱ����������ͬ���ٶ���BC��CA���յ�C��A�˶�������AM��BN�����ڵ�P������APB�ܳ������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ������һ�ּп˺�T�����п�ÿ������120Ԫ��T��ÿ������60Ԫ�������ڿ�չ������ڼ䣬��ͻ��ṩ�����Żݷ���������һ���п���һ��T�����ڼп˺�T���������۵�80%�����ij�ͻ�Ҫ���÷�װ������п�30����T��![]() ����
����![]() ��30����
��30����
��1�����ÿͻ��������ٹ����踶���� �� Ԫ���ú�x�Ĵ���ʽ��ʾ����
���ÿͻ��������ڹ����踶���� �� Ԫ���ú�x�Ĵ���ʽ��ʾ����
��2����![]() =40��ͨ������˵���������١����������ַ��������Ϊ���㣿
=40��ͨ������˵���������١����������ַ��������Ϊ���㣿
��3���������Żݷ�����ͬʱʹ�ã���![]() =40ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�������˵�����ɣ�
=40ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD����BEƽ����DBC�ҽ�CD���ڵ�E������BCE�Ƶ�C˳ʱ����ת����DCF��λ�������ӳ�BE��DF�ڵ�G��

��1����֤����BDG�ס�DEG��
��2����EGBG=4����BE�ij�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com