
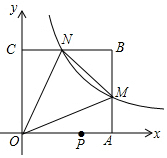
 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )| A. | 6$\sqrt{2}$ | B. | 10 | C. | 2$\sqrt{26}$ | D. | 2$\sqrt{29}$ |
分析 由正方形OABC的边长是6,得到点M的横坐标和点N的纵坐标为6,求得M(6,$\frac{k}{6}$),N($\frac{k}{6}$,6),根据三角形的面积列方程得到M(6,4),N(4,6),作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,根据勾股定理即可得到结论.
解答 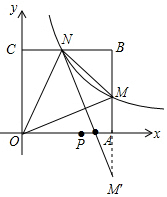 解:∵正方形OABC的边长是6,
解:∵正方形OABC的边长是6,
∴点M的横坐标和点N的纵坐标为6,
∴M(6,$\frac{k}{6}$),N($\frac{k}{6}$,6),
∴BN=6-$\frac{k}{6}$,BM=6-$\frac{k}{6}$,
∵△OMN的面积为10,
∴6×6-$\frac{1}{2}$×6×$\frac{k}{6}$-$\frac{1}{2}×$6×$\frac{k}{6}$-$\frac{1}{2}$×(6-$\frac{k}{6}$)2=10,
∴k=24,
∴M(6,4),N(4,6),
作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,
∵AM=AM′=4,
∴BM′=10,BN=2,
∴NM′=$\sqrt{BM{′}^{2}+B{N}^{2}}$=$\sqrt{1{0}^{2}+{2}^{2}}$=2$\sqrt{26}$,
故选C.
点评 本题考查了反比例函数的系数k的几何意义,轴对称-最小距离问题,勾股定理,正方形的性质,正确的作出图形是解题的关键.


科目:初中数学 来源: 题型:选择题
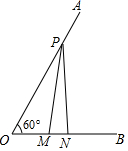 如图,已知∠AOB=60°,点P在边OA上,OP=10,点M、N在边OB上,PM=PN,若MN=2,则OM=( )
如图,已知∠AOB=60°,点P在边OA上,OP=10,点M、N在边OB上,PM=PN,若MN=2,则OM=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
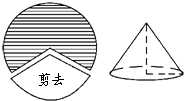 如图,将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )
如图,将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )| A. | 12cm | B. | 8cm | C. | 20cm | D. | 18cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | $-\frac{1}{4}$ | D. | $\frac{7}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
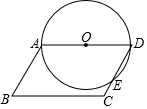 如图,?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则$\widehat{DE}$的长为( )
如图,?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则$\widehat{DE}$的长为( )| A. | $\frac{1}{3}$π | B. | $\frac{2}{3}$π | C. | $\frac{7}{6}$π | D. | $\frac{4}{3}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
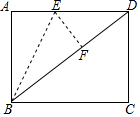 如图,在矩形ABCD中BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是( )
如图,在矩形ABCD中BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是( )| A. | 3 | B. | $\frac{24}{5}$ | C. | 5 | D. | $\frac{89}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com