
【题目】甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
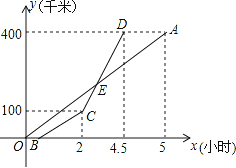
(1)求线段CD对应的函数表达式;
(2)求E点的坐标,并解释E点的实际意义;
(3)若已知轿车比货车晚出发2分钟,且到达乙地后在原地等待货车,则当x= 小时,货车和轿车相距30千米.
【答案】(1)y=120x-140(2≤x≤4.5);(2)E点的坐标为(3.5,280),即表示当货车出发3.5小时时货车和轿车相遇;(3)![]() 、
、![]() 、
、![]() 、
、![]() .
.
【解析】
试题(1)设线段CD对应的函数解析式为y=kx+b,由待定系数法求出其解即可;
(2)根据两图象相交的交点指的是两车相遇解答即可.
(3)先由货车和轿车相距30千米列出方程解答即可.
试题解析:(1)设线段CD对应的函数解析式为y=kx+b,
可得:![]() ,
,
解得:![]() .
.
所以线段CD对应的函数表达式为:y=120x-140(2≤x≤4.5);
(2)由图象可得:直线OA的解析式为:y=80x,
根据两图象相交的交点指的是两车相遇,
可得:80x=120x-140,
解得:x=3.5,
把x=3.5代入y=80x,得:y=280;
所以E点的坐标为(3.5,280),即表示当货车出发3.5小时时货车和轿车相遇;
(3)设货车出发xh后,
可得:120x-140-30=80x,
解得:x=4.25.
故答案为:4.25.
(3)由题意知,B(![]() ,0),
,0),
∴BC段解析式为y=60x-20(![]() ≤x≤2),
≤x≤2),
货车与轿车相距30km有四种情况:
1)当![]() ≤x≤2时,80x-(60x-20)=30,解得x=
≤x≤2时,80x-(60x-20)=30,解得x=![]() ;
;
2)当2<x≤![]() 时,80x-(120x-140)=30,解得x=
时,80x-(120x-140)=30,解得x=![]() ;
;
3)当![]() <x≤
<x≤![]() 时,120x-140-80x=30,解得x=
时,120x-140-80x=30,解得x=![]() ;
;
4)当![]() <x≤5时,400-80x=30,解得x=
<x≤5时,400-80x=30,解得x=![]() ;
;
∴x=![]() 、
、![]() 、
、![]() 、
、![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读材料:
某些代数恒等式可用一些卡片拼成的图形的面积来解释.例如,图①可以解释![]() ,因此,我们可以利用这种方法对某些多项式进行因式分解.
,因此,我们可以利用这种方法对某些多项式进行因式分解.
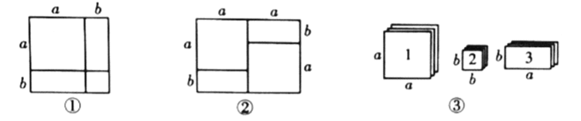
根据阅读材料回答下列问题:
(1)如图②所表示的因式分解的恒等式是________________________.
(2)现有足够多的正方形和长方形卡片(如图③),试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的长方形(每两张卡片之间既不重叠,也无空隙),使该长方形的面积为![]() ,并利用你画的长方形的面积对
,并利用你画的长方形的面积对![]() 进行因式分解.
进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,![]() 的平分线AE交CD于点F交BC的延长线于点E.
的平分线AE交CD于点F交BC的延长线于点E.
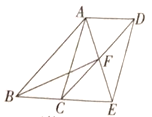
(1)求证:![]() ;
;
(2)连接BF、AC、DE,当![]() 时,求证:四边形ACED是平行四边形.
时,求证:四边形ACED是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平画直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,将直线
,将直线![]() 沿
沿![]() 轴向右平移2个单位长度交
轴向右平移2个单位长度交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,交直线
,交直线![]() 于
于![]() .
.

(1)直接写出直线![]() 的解析式为______,
的解析式为______,![]() ______.
______.
(2)在直线![]() 上存在点
上存在点![]() ,使
,使![]() 是
是![]() 的中线,求点
的中线,求点![]() 的坐标;
的坐标;
(3)如图2,在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在2015年至2017年期间销售一种礼盒。2015年,该商店用3 500元购进了这种礼盒并且全部售完;2017年,这种礼盒的进价比2015年下降了11元/盒,该商店用2 400元购进了与2015年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)2015年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定,若关于 x 的一元一次方程 ax=b 的解为 x=ba,则称该方程的为差解方程,例如:3x=![]() 的解为x=
的解为x=![]() 且
且![]() =
=![]() -3,则该方程3x=
-3,则该方程3x=![]() 就是差解方程.
就是差解方程.
请根据以上规定解答下列问题
(1)若关于 x 的一元一次方程-5x=m+1 是差解方程,则 m=_____.
(2)若关于 x 的一元一次方程 2x=ab+3a+1 是差解方程,且它的解为 x=a,求代数式(ab+2)2019的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设双曲线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() 在第三象限),将双曲线在第一象限的一支沿射线
在第三象限),将双曲线在第一象限的一支沿射线![]() 的方向平移,使其经过点
的方向平移,使其经过点![]() ,将双曲线在第三象限的一支沿射线
,将双曲线在第三象限的一支沿射线![]() 的方向平移,使其经过点
的方向平移,使其经过点![]() ,平移后的两条曲线相交于点
,平移后的两条曲线相交于点![]() ,
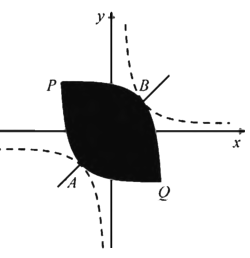
,![]() 两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,
两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,![]() 为双曲线的“眸径”.当双曲线
为双曲线的“眸径”.当双曲线![]() 的眸径为6时,
的眸径为6时,![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.

(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
如图,根据给出的数轴,解答下面的问题:
![]()
(1)已知点![]() 表示的数分别为6,-4,观察数轴,与点
表示的数分别为6,-4,观察数轴,与点![]() 距离为5的点所表示的数是 ,
距离为5的点所表示的数是 ,![]() 两点之间的距离为 ;
两点之间的距离为 ;
(2)若点![]() 到点
到点![]() ,点
,点![]() 的距离相等,观察数轴并结合所学知识求点
的距离相等,观察数轴并结合所学知识求点![]() 表示的数;
表示的数;
(3)在(2)的条件下,若动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为
出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() 秒.则点
秒.则点![]() 表示的数是多少(用含字母
表示的数是多少(用含字母![]() 的式子表示);当
的式子表示);当![]() 等于多少秒时,
等于多少秒时,![]() 之间的距离为3个单位长度.
之间的距离为3个单位长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com