
【题目】已知数轴上有A、B、C三个点对应的数分别是a、b、c,满足|a+24|+|b+10|+(c﹣10)2=0;动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在返回过程中,当t=_____秒时,P、Q两点之间的距离为2.
![]()
【答案】2或14或16
【解析】
分0<t≤10、10<t≤34和15<t≤34三种情况考虑,根据两点间的距离公式结合PQ=2即可得出关于t的一元一次方程,解之即可得出结论.
![]() ,
,
∴a+24=0,b+10=0,c-10=0,
解得a=-24,b=-10, c=10.
∴A、B、C三点分别表示的数是-24,-10,10,
经过t秒后,点P表示的数为t-24,点Q表示的数为
![]()
t-24=3(t-10)-24,
解得:t=15,
∴当t=15秒时,点Q追上点P.
(i)当0<t≤10时,点Q还在点A处,
∴PQ=t-2-(-24)=t=2;
(ii)当10<t≤34时,点P在点Q的右侧,
∴(t-24)-[3(t-10)-24]=2,
解得:t=14;
(iii)当15<t≤34时,点P在点Q的左侧,
∴3(t-10)-24-(t-24)=2,
解得:t=16.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将一块腰长为 ![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.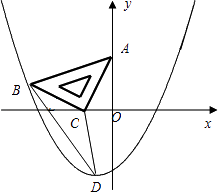
(1)点A的坐标为 , 点B的坐标为;
(2)抛物线的解析式为;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数1至2018按一定规律排列如下表:
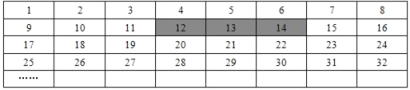
平移表中带阴影的方框,方框中三个数的和可能是( )
A. 2018 B. 2019 C. 2040 D. 2049
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A=2x2+ax﹣5y+b,B=bx2﹣![]() x﹣
x﹣![]() y﹣3.
y﹣3.
(1)求3A﹣(4A﹣2B)的值;
(2)当x取任意数值,A﹣2B的值是一个定值时,求(a+![]() A)﹣(2b+
A)﹣(2b+![]() B)的值.
B)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P(a,a)是反比例函数y= ![]() 在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在x轴上,则△POA的面积是( )
在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在x轴上,则△POA的面积是( ) 
A.3
B.4
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC= ![]() .
. 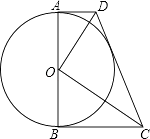
(1)求OD、OC的长;
(2)求证:△DOC∽△OBC;
(3)求证:CD是⊙O切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C,且与OA交于点E,与OB交于点F,连接CE,CF. 
(1)求证:AB与⊙O相切.
(2)若∠AOB=∠ECF,试判断四边形OECF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com