Question

为了探索代数式的最小值，

小张巧妙的运用了数学思想．具体方法是这样的：如图，C为线段BD上一动点，分别过点B、D作，连结AC、EC．已知AB=1，DE=5，BD=8，设BC=x．则， 则问题即转化成求AC+CE的最小值．

(1)我们知道当A、C、E在同一直线上时，AC+CE的值最小，于是可求得的最小值等于       ，此时        ；

(2)题中“小张巧妙的运用了数学思想”是指哪种主要的数学思想?

(选填：函数思想，分类讨论思想、类比思想、数形结合思想)

(3)请你根据上述的方法和结论，试构图求出代数式的最小值.

 

Answer 1

【答案】

（1）10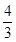，；（2）数形结合思想；（3）13.

【解析】

试题分析：（1）根据两点之间线段最短可知AC+CE的最小值就是线段AE的长度．过点E作EF∥BD，交AB的延长线于F点．在Rt△AEF中运用勾股定理计算求解．

（2）小张巧妙的运用了数形结合思想.

（3）由（1）的结果可作BD=12，过点A作AF∥BD，交DE的延长线于F点，使AB=2，ED=3，连接AE交BD于点C，然后构造矩形AFDB，Rt△AFE，利用矩形的直角三角形的性质可求得AE的值就是代数式的最小值.

试题解析：（1）过点E作EF∥BD，交AB的延长线于F点，

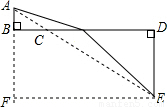
根据题意，四边形BDEF为矩形．

AF=AB+BF=5+1=6，EF=BD=8．

∴．

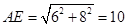即AC+CE的最小值是10．

∵EF∥BD，

∴，

∴，

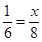解得：．

（3）过点A作AF∥BD，交DE的延长线于F点，

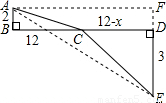
根据题意，四边形ABDF为矩形．

EF=AB+DE=2+3=5，AF=DB=12．

∴

即AC+CE的最小值是13．

考点: 轴对称-最短路线问题．