
请你在纸上画一个等腰三角形ABC(如图),使得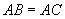 .
.
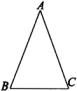
(1)请你判断一下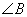 与
与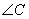 有什么大小关系呢?你的依据是什么?
有什么大小关系呢?你的依据是什么?
(2)请你再深入地思考一个问题:若只知道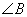 与
与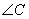 相等,请你判断一下这个三角形是什么形状的呢?并说明你的探索思路.
相等,请你判断一下这个三角形是什么形状的呢?并说明你的探索思路.
(3)由第(2)你会得到一个什么结论呢?请用一句话概括出来.
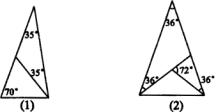
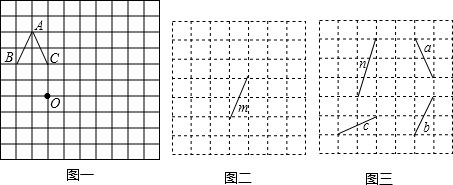
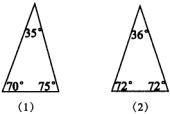
(4)现在给出两个三角形(如图),请你把图(1)分割成两个等腰三角形,把图(2)分割成三个等腰三角形.动动脑筋呀!
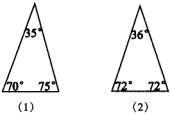
(1)相等、依据,等腰三角形两底角相等;
(2)等腰三角形;
(3)两个底角相等的三角形是等腰三角形;
(4)如图.
【解析】本题考查的是等腰三角形的性质和判定
试题分析:(1)根据“等边对等角”即可判断;
(2)过点A作 ,根据“AAS”证得
,根据“AAS”证得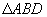 ≌
≌ ,即得结论;
,即得结论;
(3)由(2)可得结论:两个底角相等的三角形是等腰三角形;
(4)根据两个底角相等的三角形是等腰三角形,以及三角形的内角和定理进行分割即可。
(1)相等、依据,等腰三角形两底角相等;
(2)等腰三角形.
如图,
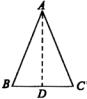
证明:过点A作 ,
,
在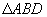 和
和 中,
中,
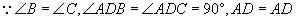 ,
,
∴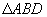 ≌
≌ ,
,
∴ ;
;
(3)两个底角相等的三角形是等腰三角形;
(4)如图.

考点:本题考查的是等腰三角形的性质和判定
点评:解答本题的关键是掌握好等腰三角形的性质和判定,注意分割等腰三角形时,要注意两点:①有两个角相等;②内角和是180°.


科目:初中数学 来源: 题型:
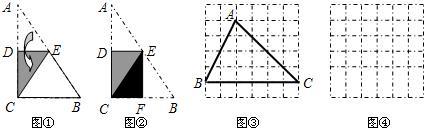
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2012年北师大版初中数学七年级下7.2简单的轴对称图形练习卷(解析版) 题型:解答题
请你在纸上画一个等腰三角形ABC(如图),使得AB=AC.
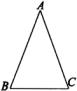
(1)请你判断一下∠B与∠C有什么大小关系呢?你的依据是什么?
(2)请你再深入地思考一个问题:若只知道∠B与∠C相等,请你判断一下这个三角形是什么形状的呢?并说明你的探索思路.
(3)由第(2)你会得到一个什么结论呢?请用一句话概括出来.
(4)现在给出两个三角形(如图),请你把图(1)分割成两个等腰三角形,把图(2)分割成三个等腰三角形.动动脑筋呀!
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com