
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与x轴交于点A和点B(点A在点B左侧),
与x轴交于点A和点B(点A在点B左侧),
(1)若抛物线的对称轴是直线x=1,求出点A和点B的坐标,并画出此时函数的图象;
(2)当已知点P(m,2),Q(-m,2m-1).若抛物线与线段PQ恰有一个公共点,结合函数图象,求m的取值范围.
【答案】(1)点A坐标为(-1,0),点B坐标为(3,0),图像见解析;(2)m≤-2 或m≥1
【解析】
(1)根据抛物线的对称轴是直线x=1可得![]() =1,求出m=2,得
=1,求出m=2,得![]() ,求出与x轴的交点坐标,根据点A在点B左侧即可求得点A,点B的坐标;
,求出与x轴的交点坐标,根据点A在点B左侧即可求得点A,点B的坐标;
(2)根据点Q在点D上方或与点D重合时,抛物线与线段PQ恰有一个公共点得![]() ,结合图象求解即可.
,结合图象求解即可.
(1)∵抛物线的对称轴为:x=![]() =
=![]() =1
=1
∴m=2
∴抛物线为:![]()
将y=0代入,得![]()
解得:![]() =-1,
=-1,![]() =3,
=3,
∵点A在点B左侧
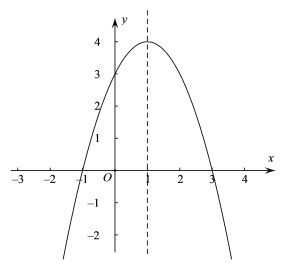
∴点A坐标为(-1,0),点B坐标为(3,0),
(2)m≤-2 或m≥1
将![]() 代入
代入![]() ,得
,得![]()
∴抛物线过定点C(m,3)
∵点P(m,2)
∴点P在点C下方,如图,
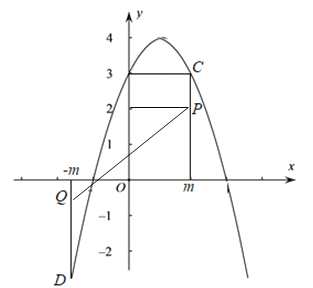
将![]() 代入
代入![]() ,得
,得![]() ,则
,则![]()
∴点Q在点D上方或与点D重合时,抛物线与线段PQ恰有一个公共点
∴![]()
整理得![]()
设![]() ,画图象如图:
,画图象如图:

当y=0时,![]() ,解得,
,解得,![]() ,
,![]() ,
,
∴抛物线![]() 与x轴的交点坐标为(-2,0),(1,0)
与x轴的交点坐标为(-2,0),(1,0)
∴当![]() 或
或![]() 时,
时,![]()
所以,抛物线与线段PQ恰有一个公共点,m的取值范围是![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,连接AP,交CD于点M,若∠ACD=110°,则∠CMA的度数为( )
EF长为半径作圆弧,两条圆弧交于点P,连接AP,交CD于点M,若∠ACD=110°,则∠CMA的度数为( )
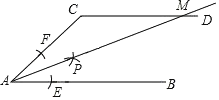
A.30°B.35°C.70°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察下列图形与等式的关系,并填空:
第一个图形: ;
;
第二个图形: ;
;
第一个等式:9+4=13;第二个等式:13+8=21;
第三个图形: ;……;
;……;
第三个等式: + = ;……;
(2)根据以上图形与等式的关系,请你猜出第n个等式(用含有n的代数式表示),并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转90°得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF,CF.

(1)如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形;
(2)如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由;
(3)在(2)的条件下,四边形PCFE的面积是否有最大值?若有,请求出面积的最大值及此时BP长;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,过点A作AE⊥BC于点E,点F在边AD上,且DF=BE,连接DE,CF.
(1)求证:四边形AECF是矩形;
(2)若DE平分∠ADC,AB=5,AD=8,求tan∠ADE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,直线EF分别交直线AB、CD于点G、H,GI、HI分别平分∠BGH、∠GHD.
(1)求证GI⊥HI.
(2)请用文字概括(1)所证明的命题: .
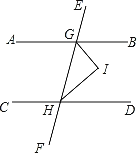
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD.
(1)作∠B的平分线交AD于E点。(用尺规作图法,保留作图痕迹,不要求写作法);
(2)若ABCD的周长为10,CD=2,求DE的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
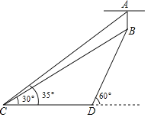
【题目】如图,宾馆大厅的天花板上挂有一盏吊灯AB,某人从C点测得吊灯顶端A的仰角为![]() ,吊灯底端B的仰角为
,吊灯底端B的仰角为![]() ,从C点沿水平方向前进6米到达点D,测得吊灯底端B的仰角为
,从C点沿水平方向前进6米到达点D,测得吊灯底端B的仰角为![]() .请根据以上数据求出吊灯AB的长度.(结果精确到0.1米.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,
.请根据以上数据求出吊灯AB的长度.(结果精确到0.1米.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
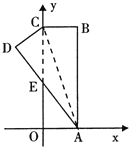
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E。那么点D的坐标为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com