
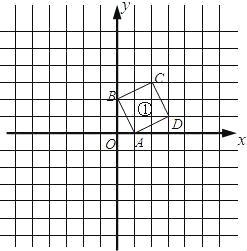
����Ŀ����ƽ��ֱ������ϵ�У���A��1��0����B��0��2����C��2��3����D��3��1�����߶��������������γ�һ��ͼ����ͼ����������ͼ�����Ƶ�O��ʱ����ת90���õ�ͼ�������Ե�OΪλ�����ģ�λ�Ʊ�Ϊ1��2��ͼ������λ�����ĵ������зŴ�õ�ͼ������
��1��������ϵ�зֱ�ͼ������ͼ������
��2������D��ͼ�����ж�Ӧ�ĵ��Ϊ��E����ͼ�����ж�Ӧ�ĵ��Ϊ��F����S��DEF= ��
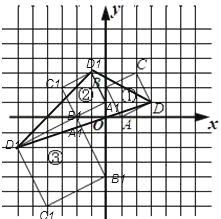
��3����ͼ��������һ��P��A��B���⣩������Ϊ��a��b����ͼ��������֮��Ӧ�ĵ��Ϊ��Q��ͼ��������֮��Ӧ�ĵ��Ϊ��R����S��PQR= �����ú���a��b�Ĵ���ʽ��ʾ��
���𰸡���1����ͼ�μ���������2��15����3��![]() ��a2+b2��.
��a2+b2��.
��������
�����������1����ͼ�����еĸ������Ƶ�O��ʱ����ת90���õ�֪����Ķ�Ӧ�㣬˳�����Ӷ�Ӧ��õ�ͼ�������Ե�OΪλ�����ģ�λ�Ʊ�Ϊ1��2��ͼ������λ�����ĵ������зŴ�õ�ͼ������������OA��OB��OC��OD�����ӳ���A����B����C����D����ʹOA����OB����OC����OD����OA��OB��OC��OD��2����˳�����Ӹ��㼴�ɣ���2�������������S��DEF�����ļ���ͼ����ɣ����������ʽ���㣮��ͼ�пɿ����������Ǿ��ε���������������ε����������S��DEF=9��5��4��2��2��5��5��2��9��3��2=15����3����������C������P,P��a��b������Q�����꣨-b,a��,R������Ϊ��-2a,-2b��,���ȴ�ͼ���ҳ���������ε����㣬Ȼ����������������Σ��۲�����õ������ε������ʽ=������3�������ε�������г�ʽ�Ӽ��㣮
�����������1����ͼ�����еĸ������Ƶ�O��ʱ����ת90���õ���������Ķ�Ӧ�㣬˳�����Ӷ�Ӧ��õ�ͼ�������Ե�OΪλ�����ģ�λ�Ʊ�Ϊ1��2��ͼ������λ�����ĵ������зŴ�õ�ͼ������������OA��OB��OC��OD�����ӳ���A����B����C����D����ʹOA����OB����OC����OD����OA��OB��OC��OD��2����˳�����Ӹ��㣬��ͼ����ͼ����
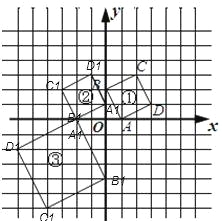
��2����ͼ�пɿ���������DEF������Ǿ��ε���������������ε����������S��DEF=9��5��4��2��2��5��5��2��9��3��2=15����3������P���ڵ�һ�����ڣ�������Ϊ��a��b��������Q������Ϊ��-b��a������R������Ϊ��-2a��-2b����������a��b��S��PQR=��2a+a����a+2b��-![]() (2a-b)(2b+a)-
(2a-b)(2b+a)-![]() (a+b)(a-b)-
(a+b)(a-b)-![]() (2a+a)(2b+b)=3a2+6ab-
(2a+a)(2b+b)=3a2+6ab-![]() (2a2-2b2+3ab+a2-b2+9ab)=3a2+6ab-
(2a2-2b2+3ab+a2-b2+9ab)=3a2+6ab-![]() a2+
a2+![]() b2-6ab=
b2-6ab=![]() ��a2+b2��.
��a2+b2��.


 ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д� �㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ab��0����a��b��0��������ѡ���У���ȷ���ǣ�������
A. a��0��b��0 B. a��0��b��0 C. a��0��b��0 D. a��0��b��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y��2��x��3��2+2��ͼ������������ȷ���ǣ�������
A. ������������3��2��
B. ��������
C. ��x��3ʱ��y��x�����������
D. �Գ�����ֱ��y����3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
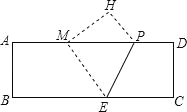
����Ŀ����ͼ���ھ���ֽƬABCD�У�AB=4��AD=12��������ֽƬ�۵���ʹ��C����AD���ϵĵ�M�����ۺ�ΪPE����ʱPD=3��
��1����MP��ֵ��
��2����AB������һ������F���Ҳ����A��B�غϣ���AF���ڶ���ʱ����MEF���ܳ���С��
��3������G��Q��AB���ϵ��������㣬�Ҳ����A��B�غϣ�GQ=2�����ı���MEQG���ܳ���Сʱ������С�ܳ�ֵ�����������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������εĽ�ƽ���ߣ�������( ).
A. �����߶� B. ����ֱ��
C. �������� D. ��ƽ���ߡ����������ߡ������߶�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������������ǣ� ��
A.��һ������ֻ��һ��ֱ������ֱ֪��ƽ��
B.��ֱ��l�Ͻ�ȡһ���߶�AB��ʹAB=3cm
C.��ͬһ����ϵ�ڣ�ֱ��y=2x+3��ֱ��y=x+3ƽ��
D.�����ε�һ����Ǵ�������һ���ڽ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com