
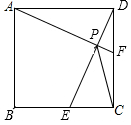
 如图,正方形ABCD中,点E为BC的中点,作AF⊥DE交DE、DC分别于P、F点,连PC.
如图,正方形ABCD中,点E为BC的中点,作AF⊥DE交DE、DC分别于P、F点,连PC.分析 (1)由△ADF≌DCE,推出DF=CE,由EC=$\frac{1}{2}$BC,BC=DC,推出DF=$\frac{1}{2}$DC,即可证明F点为DC的中点;
(2)如图作CM⊥CP交PE的延长线于M.只要证明△PCF≌△MCE,推出PF=EM,PC=CM,推出△PCM是等腰直角三角形,即可解决问题;
解答 证明:(1)∵四边形ABCD是正方形,
∴AD=CD=BC,∠ADC=∠C=90°,
∵AF⊥DE,
∴∠APD=∠DPF=90°,
∴∠ADP+∠DAF=90°,∠ADP+∠EDC=90°,
∴∠DAF=∠EDC,
在△ADF和△DCE中,
$\left\{\begin{array}{l}{∠DAF=∠EDC}\\{∠ADF=∠C}\\{AD=CD}\end{array}\right.$,
∴△ADF≌DCE,
∴DF=CE,
∵EC=$\frac{1}{2}$BC,BC=DC,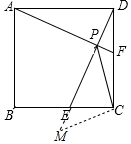
∴DF=$\frac{1}{2}$DC,
∴F点为DC的中点;
(2)如图作CM⊥CP交PE的延长线于M.
∵△ADF≌△DCE,
∴∠AFD=∠DEC,
∴∠PFC=∠CEM,
∵∠PCM=∠DCB=90°,
∴∠PCF=∠ECM,∵CF=CE,
∴△PCF≌△MCE,
∴PF=EM,PC=CM,
∴△PCM是等腰直角三角形,
∴PM=$\sqrt{2}$PC,
∴PE+EM=PE+PF=$\sqrt{2}$PC,
∴PE+PF=$\sqrt{2}$PC.
点评 本题考查正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,学会添加常用辅助线,构造全等三角形.


科目:初中数学 来源: 题型:解答题
| A | B | |
| 进价(万元/套) | 1.5 | 1.2 |
| 售价(万元/套) | 1.65 | 1.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某体育用品商场为了推销一种品牌运动服,先做了市场调查,得到数据如下表:
某体育用品商场为了推销一种品牌运动服,先做了市场调查,得到数据如下表:| 卖出价格x(元/件) | 50 | 51 | 52 | 53 |
| 销售量p(件) | 500 | 490 | 480 | 470 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
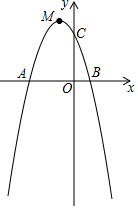 如图,抛物线与x轴交于点A(-3,0),B(1,0)两点,与y轴交于点C(0,3).
如图,抛物线与x轴交于点A(-3,0),B(1,0)两点,与y轴交于点C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)在同一平面直角坐标系中描出下列各点,并将各点用线段依次连接起来:
(1)在同一平面直角坐标系中描出下列各点,并将各点用线段依次连接起来:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com