
| A. | 3a2b-a2b=2 | |
| B. | 使式子$\sqrt{x+2}$有意义的x的取值范围是x>-2 | |
| C. | 单项式-x2的系数是-1 | |
| D. | 若分式$\frac{{{a^2}-1}}{a+1}$的值等于0,则a=±1 |
分析 根据合并同类项法则,分式有意义,被开方数大于等于0,单项式的系数,分式的值为0,分子等于0,分母不等于0对各选项分析判断即可得解.
解答 解:A、3a2b-a2b=2a2b,故本选项错误;
B、由题意得,x+2≥0,
解得x≥-2,故本选项错误;
C、单项式-x2的系数是-1正确,故本选项正确;
D、分式的值等于0,则a2-1=0且a+1≠0,
解得a=±1且a≠-1,
所以,a=1,故本选项错误.
故选C.
点评 此题考查了二次根式的意义和性质.概念:式子$\sqrt{a}$(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义,还考查了分式的值为0的条件以及合并同类项法则.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
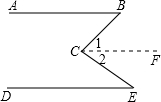 如图,AB∥DE,试问∠B,∠E,∠BCE有什么关系
如图,AB∥DE,试问∠B,∠E,∠BCE有什么关系查看答案和解析>>
科目:初中数学 来源: 题型:解答题
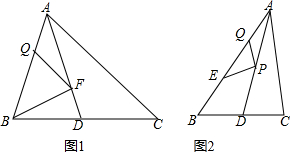
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
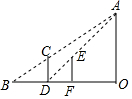 如图,墨墨和茗茗在晚上利用灯光下自己的影长来测量路灯AO的高度,当墨墨在点D处时.茗茗测得墨墨的身高CD与影子BD的长正好相等,接着墨墨沿BO方向走,走到点F处时,墨墨身高EF的影子恰好是线段DF.已知DF=1.2m,墨墨的身高为1.8m,则路灯AO的高度为( )
如图,墨墨和茗茗在晚上利用灯光下自己的影长来测量路灯AO的高度,当墨墨在点D处时.茗茗测得墨墨的身高CD与影子BD的长正好相等,接着墨墨沿BO方向走,走到点F处时,墨墨身高EF的影子恰好是线段DF.已知DF=1.2m,墨墨的身高为1.8m,则路灯AO的高度为( )| A. | 5m | B. | 5.4m | C. | 5.6m | D. | 5.8m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
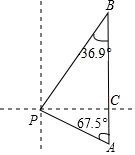 马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西36.9°方向,求轮船行驶过程中与小岛P的最短距离PC.
马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西36.9°方向,求轮船行驶过程中与小岛P的最短距离PC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
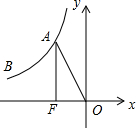 如图,已知反比例函数的图象经过点A(-2,4)、B(m,2),过点A作AF⊥x轴于点F,连接OA.
如图,已知反比例函数的图象经过点A(-2,4)、B(m,2),过点A作AF⊥x轴于点F,连接OA.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
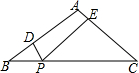 △ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )
△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )| A. | 4.8 | B. | 4.8或3.8 | C. | 3.8 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com