
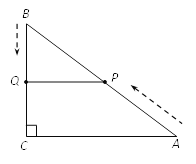
【题目】如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm. 点P从点A出发,沿AB边以2 cm/s的速度向点B匀速移动;点Q从点B出发,沿BC边以1 cm/s的速度向点C匀速移动, 当一个运动点到达终点时,另一个运动点也随之停止运动,设运动的时间为t(s).
(1)当PQ∥AC时,求t的值;
(2)当t为何值时,△PBQ的面积等于![]() cm 2.
cm 2.
【答案】(1)t=![]() ;(2)当t为2s或3s时,△PBQ的面积等于
;(2)当t为2s或3s时,△PBQ的面积等于![]() cm 2.
cm 2.
【解析】
(1)根据PQ∥AC得到△PBQ∽△ABC,列出比例式即可求解;
(2)解法一:过点Q作QE⊥AB于E,利用△BQE∽△BCA,得到![]() ,得到QE=
,得到QE=![]() t,根据S△PBQ =
t,根据S△PBQ =![]() BP·QE=
BP·QE=![]() 列出方程即可求解;
列出方程即可求解;
解法二:过点P作PE⊥BC于E,则PE∥AC,得到△BPE∽△BAC,则![]() ,求出PE=
,求出PE=![]() (10-2t).,利用S△PBQ =
(10-2t).,利用S△PBQ =![]() BQ·PE=
BQ·PE=![]() 列出方程即可求解.
列出方程即可求解.
(1)由题意得,BQ= tcm,AP=2 cm,则BP=(10—2t)cm
在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm
![]()
∵ PQ∥AC, ∴ △PBQ∽△ABC,
∴ ![]() ,即
,即 ![]() ,
,
解得 t=![]() .
.
(2)解法一:
如图3,过点Q作QE⊥AB于E,则∠QEB =∠C=90°.
∵ ∠B =∠B,∴ △BQE∽△BCA,
∴ ![]() ,即
,即 ![]() , 解得 QE=
, 解得 QE=![]() t.
t.
∴ S△PBQ =![]() BP·QE=
BP·QE=![]() , 即
, 即![]() ·(10-2t)·
·(10-2t)·![]() t =
t =![]() .
.
整理,得t2-5t+6=0. 解这个方程,得t1=2,t2=3.
∵ 0<t<5,∴ 当t为2s或3s时,△PBQ的面积等于![]() cm 2.
cm 2.
解法二:过点P作PE⊥BC于E,则PE∥AC(如图4).
∵ PE∥AC.
∴ △BPE∽△BAC,
∴ ![]() ,即
,即 ![]() , 解得 PE=
, 解得 PE=![]() (10-2t).
(10-2t).
∴ S△PBQ =![]() BQ·PE=
BQ·PE=![]() , 即
, 即![]() ·t·
·t·![]() (10-2t)=
(10-2t)=![]()
整理,得t2-5t+6=0. 解这个方程,得t1=2,t2=3.
∵ 0<t<5,
∴ 当t为2s或3s时,△PBQ的面积等于![]() cm 2.
cm 2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像经过点
的图像经过点![]() (1,0).
(1,0).
(1)当![]() ,
,![]() 时,求二次函数的解析式及二次函数最小值;
时,求二次函数的解析式及二次函数最小值;
(2)二次函数的图像经过点![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() ).若对任意实数
).若对任意实数![]() ,函数值
,函数值![]() 都不小于
都不小于![]() ,求此时二次函数的解析式.
,求此时二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6,AD=8,点E是边AD上一点,EM⊥BC交AB于点M,点N在射线MB上,且AE是AM和AN的比例中项.
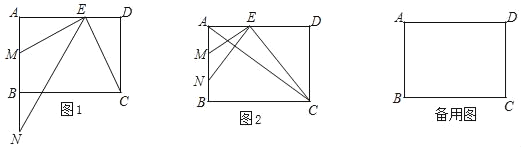
(1)如图1,求证:∠ANE=∠DCE;
(2)如图2,当点N在线段MB之间,联结AC,且AC与NE互相垂直,求MN的长;
(3)连接AC,如果△AEC与以点E、M、N为顶点所组成的三角形相似,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是⊙
是⊙![]() 的弦,
的弦,![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 的直线交
的直线交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() 是⊙
是⊙![]() 的切线.
的切线.
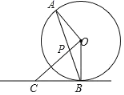
(1)判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)若![]() ,求
,求![]() 的长;
的长;
(3)设![]() 的面积是
的面积是![]() 的面积是
的面积是![]() ,且
,且![]() .若⊙
.若⊙![]() 的半径为
的半径为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】富平因取“富庶太平”之意而得名,是华夏文明重要发祥地之一.某班举行关于“美丽的富平”的演讲活动.小明和小丽都想第一个演讲,于是他们通过做游戏来决定谁第一个来演.讲游戏规则是:在一个不透明的袋子中有一个黑球a和两个白球b、c,(除颜色外其它均相同),小丽从袋子中摸出一个球,放回后搅匀,小明再从袋子中摸出一个球,若两次摸到的球颜色相同,则小丽获胜,否则小明获胜,请你用树状图或列表的方法分别求出小丽与小明获胜的概率,并说明这个游戏规则对双方公平吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC.求作⊙O,使得点O在边AB上,且⊙O经过B、D两点;并证明AC与⊙O相切.(尺规作图,保留作图痕迹,不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com