
(本题10分)已知,如图,过点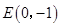 作平行于
作平行于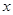 轴的直线
轴的直线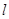 ,抛物线
,抛物线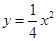 上的两点
上的两点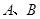 的横坐标分别为
的横坐标分别为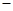 1和4,直线
1和4,直线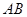 交
交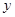 轴于点
轴于点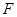 ,过点
,过点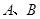 分别作直线
分别作直线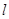 的垂线,垂足分别为点
的垂线,垂足分别为点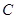 、
、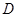 ,连接
,连接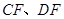 .
.
【小题1】(1)求点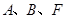 的坐标;
的坐标;
【小题2】(2)求证: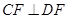 ;
;
【小题3】(3)点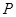 是抛物线
是抛物线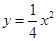 对称轴右侧图象上的一动点,过点
对称轴右侧图象上的一动点,过点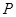 作
作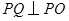 交
交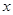 轴于点
轴于点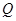 ,是否存在点
,是否存在点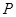 使得
使得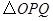 与
与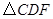 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点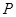 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【小题1】(1).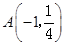
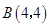
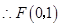
【小题2】(2) 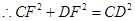
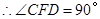

【小题3】(3)
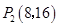
解析考点:二次函数综合题。
分析:
(1)有两种方法,方法一是传统的点的待定系数法,方法二,通过作辅助线,构造△BGF∽△BHA由比例关系求出F点坐标;
(2)也有两种方法,方法一,在Rt△CEF中算出△DEF边长利用勾股定理证明CF⊥DF;方法二利用几何关系求出∠CFD=90°;
(3)求存在性问题,先假设存在,看是否找到符合条件的点P的坐标,此题分两种情况;①Rt△QPO∽Rt△CFD;②Rt△OPQ∽Rt△CFD,根据比例求出P点坐标。
解答: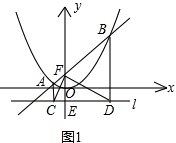
(1)方法一:如图1,当x=-1时,y=1/4;当x=4时,y=4
∴A(-1,1/4),B(4,4)。
设直线AB的解析式为y=kx+b,
则-k+b=1/4,4k+b=4
解得k=3/4,b=1。
∴直线AB的解析式为y=3/4x+1。
当x=0时,y=1
∴F(0,1)。
方法二:求A、B两点坐标同方法一,
如图2,作FG⊥BD,AH⊥BD,垂足分别为G、H,交y轴于点N,则四边FOMG和四边形NOMH均为矩形,设FO=x,
∵△BGF∽△BHA
∴BG/BH=FG/AH
∴(4- x)/(4-1/4)=4/5
解得x=1
∴F(0,1)。
(2)证明:
方法一:在Rt△CEF中,CE=1,EF=2,
根据勾股定理得:CF2=CE2+EF2=12+22=5,
∴CF=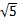
在Rt△DEF中,DE=4,EF=2
∴DF2=DE2+EF2=42+22=20
∴DF=2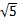
由(1)得C(-1,-1),D(4,-1)
∴CD=5
∴CD2=52=25
∴CF2+DF2=CD2
∴∠CFD=90°
∴CF⊥DF(8分)
方法二:由(1)知AF=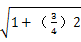 =
= ,AC=5/4
,AC=5/4
∴AF=AC。
同理:BF=BD
∴∠ACF=∠AFC
∵AC∥EF
∴∠ACF=∠CFO
∴∠AFC=∠CFO
同理:∠BFD=∠OFD
∴∠CFD=∠OFC+∠OFD=90°
即CF⊥DF(8分)
(3)存在。
解:如图3,作PM⊥x轴,垂足为点M(9分)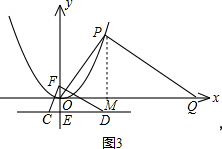
又∵PQ⊥OP
∴Rt△OPM∽Rt△OQP
∴PM/PQ=OM/OP
∴PQ/OP=PM/OM。
设P(x,1/4x2)(x>0),
则PM=1/4x2,OM=x
①当Rt△QPO∽Rt△CFD时,
PQ/OP=CF/DF=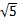 /2
/2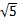 =1/2
=1/2
∴PM/OM=1/4x2/x=1/2
解得x=2
∴P1(2,1)。
②当Rt△OPQ∽Rt△CFD时,
PQ/OP=DF/CF=2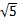 /
/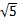 =2
=2
∴PM/OM=1/4x2/x=2
解得x=8
∴P2(8,16)
综上,存在点P1(2,1)、P2(8,16)使得△OPQ与△CDF相似。
点评:此题是一道综合性较强的题,前两问方法多,有普通的方法和新颖的方法,作合适的辅助线很重要,最后一问是探究性问题,发散思维。


科目:初中数学 来源: 题型:
(本题10分)已知一个正比例函数和一个一次函数的图象交于点P(-2,2),且一次函数的图象与y轴相交于点Q(0,4)
1.(1)求这两个函数的解析式
2.(2)在同一坐标系内,分别画出这两个函数的图象
3.(3)求出![]() 的面积
的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题10分)已知,如图,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,抛物线
,抛物线![]() 上的两点
上的两点![]() 的横坐标分别为
的横坐标分别为![]() 1和4,直线
1和4,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 分别作直线
分别作直线![]() 的垂线,垂足分别为点
的垂线,垂足分别为点![]() 、
、![]() ,连接
,连接![]() .
.
1.(1)求点![]() 的坐标;
的坐标;
2.(2)求证:![]() ;
;
3.(3)点![]() 是抛物线
是抛物线![]() 对称轴右侧图象上的一动点,过点
对称轴右侧图象上的一动点,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,是否存在点
,是否存在点![]() 使得
使得![]() 与
与![]() 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省南通市幸福中学八年级上学期期中考试数学卷 题型:解答题
(本题10分)已知:如图所示,
【小题1】(1)作出△ABC关于y轴对称的△ ,并写出△
,并写出△ 三个顶点的坐标.
三个顶点的坐标.
【小题2】(2) 在x轴上画出点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源:2012届江苏省苏州市高新区九年级上学期期末考试数学卷 题型:解答题
(本题10分)已知:直角梯形OABC中,BC//OA,∠AO C=90°,以AB为直径的OM交OC于点D、E,连结AD、BD.现以O为坐标原点,OA、OC所在直线为x轴、y轴建立如图所示直角坐标系,若抛
C=90°,以AB为直径的OM交OC于点D、E,连结AD、BD.现以O为坐标原点,OA、OC所在直线为x轴、y轴建立如图所示直角坐标系,若抛 物线y=ax2-2ax-3a(a<0)经过点A、B、D,且B为抛物线的顶点.
物线y=ax2-2ax-3a(a<0)经过点A、B、D,且B为抛物线的顶点.
【小题1】(1)写出顶点B的坐标 ▲ (用a的代数式表示);
【小题2】(2)求抛物线的解析式:
【小题3】(3)在x轴下方的抛物线上是否存在这样的点P:过点P作PN⊥x轴于N,使得△PAN与△OAD相似?若存在,求出点P的坐标:若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省苏州市高新区九年级上学期期末考试数学卷 题型:解答题
(本题10分)已知:直角梯形OABC中,BC//OA,∠AOC=90°,以AB为直径的OM交OC于点D、E,连结AD、BD.现以O为坐标原点,OA、OC所在直线为x轴、y轴建立如图所示直角坐标系,若抛物线y=ax2-2ax-3a(a<0)经过点A、B、D,且B为抛物线的顶点.

1.(1)写出顶点B的坐标 ▲ (用a的代数式表示);
2.(2)求抛物线的解析式:
3.(3)在x轴下方的抛物线上是否存在这样的点P:过点P作PN⊥x轴于N,使得△PAN与△OAD相似?若存在,求出点P的坐标:若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com