
 如图,在△ABC中,AB=3,AC=$\frac{9}{4}$,点D是BC边上的一点,AD=BD=2DC,设△ABD与△ACD的内切圆半径分别为r1,r2,那么$\frac{r_1}{r_2}$=( )
如图,在△ABC中,AB=3,AC=$\frac{9}{4}$,点D是BC边上的一点,AD=BD=2DC,设△ABD与△ACD的内切圆半径分别为r1,r2,那么$\frac{r_1}{r_2}$=( )| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
分析 如图,设⊙O与△ABD内切于E、F、G.首先证明AE=BE=BF=AG=$\frac{3}{2}$,设DF=DG=m,由AD=2DC,推出CD=$\frac{1}{2}$($\frac{3}{2}$+m),由S△ABD:S△ADC=BD:DC=2:1,
可得$\frac{1}{2}(3+3+2m)•{r}_{1}$:$\frac{1}{2}$[$\frac{9}{4}$+$\frac{3}{2}(\frac{3}{2}+m)$]•r2=2:1,由此即可得出结论.
解答 解:如图,设⊙O与△ABD内切于E、F、G.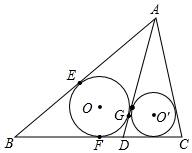
∵DA=DB,DG=DF,
∴BF=AG=BE=AE,
∵AB=3,
∴AE=BE=BF=AG=$\frac{3}{2}$,设DF=DG=m,
∵AD=2DC,
∴CD=$\frac{1}{2}$($\frac{3}{2}$+m),
∵S△ABD:S△ADC=BD:DC=2:1,
∴$\frac{1}{2}(3+3+2m)•{r}_{1}$:$\frac{1}{2}$[$\frac{9}{4}$+$\frac{3}{2}(\frac{3}{2}+m)$]•r2=2:1,
∴(6+2m)•r1:$\frac{3}{4}$(2+2m)•r2═2:1,
∴r1:r2=3:2.
故选C.
点评 本题考查三角形的内切圆与内心、切线长定理、三角形的面积公式:S=$\frac{1}{2}$(a+b+c)•r(r为内切圆半径)等知识,解题的关键是灵活运用切线长定理,学会利用参数解决问题,属于中考选择题中的压轴题.


科目:初中数学 来源: 题型:解答题
| 收费方式 | 月使用费(元) | 包时上网时间(h) | 超时费(元/min) |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
| 0≤x<25 | 25<x≤50 | x>50 | |
| 收费方式A应收取费用(元) | 30 | 3x-45 | 3x-45 |
| 收费方式B应收取费用(元) | 50 | 50 | 3x-100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
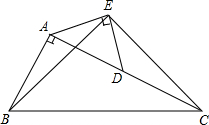 已知:如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,以AD为斜边在△ABC外作等腰直角三角形AED,连结BE、EC.试猜想线段BE和EC有何关系,并证明你的猜想.
已知:如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,以AD为斜边在△ABC外作等腰直角三角形AED,连结BE、EC.试猜想线段BE和EC有何关系,并证明你的猜想.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在等腰直角三角形ABC中,∠CAB=90°,以AB为边向外作等边△ABD,AE⊥BD,CD、AE交于点M,若DM=1,求BC的值.
如图,已知在等腰直角三角形ABC中,∠CAB=90°,以AB为边向外作等边△ABD,AE⊥BD,CD、AE交于点M,若DM=1,求BC的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:单选题
如图所示,用量角器度量一些角的度数。下列结论中正确的是( )
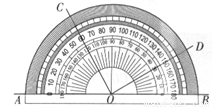
A. ∠BOC=60° B. ∠COD=150°
C. ∠AOC与∠BOD的大小相等 D. ∠AOC与∠BOD互余
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com