
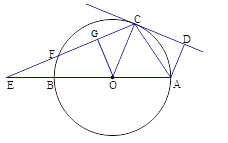
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
【答案】(1)证明见解析;(2)①∠OCE=45°;②EF =![]() -2.
-2.
【解析】【试题分析】(1)根据直线与⊙O相切的性质,得OC⊥CD.
又因为AD⊥CD,根据同一平面内,垂直于同一条直线的两条直线也平行,得:AD//OC. ∠DAC=∠OCA.又因为OC=OA,根据等边对等角,得∠OAC=∠OCA.等量代换得:∠DAC=∠OAC.根据角平分线的定义得:AC平分∠DAO.
(2)①因为 AD//OC,∠DAO=105°,根据两直线平行,同位角相等得,∠EOC=∠DAO=105°,在![]() 中,∠E=30°,利用内角和定理,得:∠OCE=45°.
中,∠E=30°,利用内角和定理,得:∠OCE=45°.
②作OG⊥CE于点G,根据垂径定理可得FG=CG, 因为OC=![]() ,∠OCE=45°.等腰直角三角形的斜边是腰长的
,∠OCE=45°.等腰直角三角形的斜边是腰长的![]() 倍,得CG=OG=2. FG=2.在Rt△OGE中,∠E=30°,得GE=
倍,得CG=OG=2. FG=2.在Rt△OGE中,∠E=30°,得GE=![]() , 则EF=GE-FG=
, 则EF=GE-FG=![]() -2.
-2.
【试题解析】
(1)∵直线与⊙O相切,∴OC⊥CD.
又∵AD⊥CD,∴AD//OC.
∴∠DAC=∠OCA.
又∵OC=OA,∴∠OAC=∠OCA.
∴∠DAC=∠OAC.
∴AC平分∠DAO.
(2)解:①∵AD//OC,∠DAO=105°,∴∠EOC=∠DAO=105°
∵∠E=30°,∴∠OCE=45°.
②作OG⊥CE于点G,可得FG=CG
∵OC=![]() ,∠OCE=45°.∴CG=OG=2.
,∠OCE=45°.∴CG=OG=2.
∴FG=2.
∵在Rt△OGE中,∠E=30°,∴GE=![]() .
.
∴EF=GE-FG=![]() -2.
-2.


科目:初中数学 来源: 题型:
【题目】王教授和他的孙子小强星期天一起去爬山,来到山脚下,小强让爷爷先上山,然后追赶爷爷,如图所示,两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(小强开始爬山时开始计时),请看图回答下列问题:
(1)爷爷比小强先上了多少米?山顶离山脚多少米?
(2)谁先爬上山顶?小强爬上山顶用了多少分钟?
(3)图中两条线段的交点表示什么意思?这时小强爬山用时多少?离山脚多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲.乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.若设甲.乙两种商品原来的单价分别为x元.y元,则可列方程组为_________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:如图1所示的图形,像我们常见的学习用品--圆规.我们不妨把这样图形叫做“规形图”,
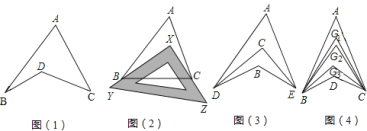
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX等于多少度;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB、AC上.

(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成矩形零件如图2,问这个矩形的最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() ,点
,点![]() ,
,![]() 分别是直线
分别是直线![]() ,
,![]() 上任意两点,在直线
上任意两点,在直线![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,在直线
,在直线![]() 上任取一点
上任取一点![]() ,作
,作![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.

(1)如图1,若点![]() 是线段
是线段![]() 上任意一点,
上任意一点,![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() ;
;
(2)如图2,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 与
与![]() 互为补角,若
互为补角,若![]() ,请判断线段
,请判断线段![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com