
分析 (1)证明△ABE≌△CBF且△BEF是等边三角形即可;
(2)延长FC至G,使AE=CG,连接BG,先证△BAE≌△BCG,再证△GBF≌△EBF即可;
(3)在AE上截取AH=CF,连接BH,先证△BAH≌△BCF,再证△EBF≌△EBH即可.
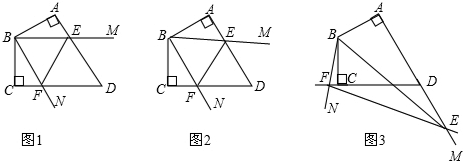
解答 解:(1)如图1,
在△ABE和△CBF中,
$\left\{\begin{array}{l}{AE=CF}\\{∠BAE=∠BCF}\\{AB=CB}\end{array}\right.$,
∴△ABE≌△CBF(SAS),
∴∠CBF=∠EBA,BE=BF,
∵∠ABC=120°,∠EBF=60°,
∴△BEF是等边三角形,CF=$\frac{1}{2}BF$,AE=$\frac{1}{2}BE$,
∴EF=BE=BF=AE+CF;
(2)如图2,延长FC至G,使AE=CG,连接BG,
在△BAE和△BCG中,
$\left\{\begin{array}{l}{BA=BC}\\{∠BAE=∠BCG}\\{AE=CG}\end{array}\right.$,
∴△BAE≌△BCG(SAS),
∴∠ABE=∠CBG,BE=BG,
∵∠ABC=120°,∠EBF=60°,
∴∠ABE+∠CBF=60°,
∴∠CBG+∠CBF=60°,
∴∠GBF=∠EBF,
在△GBF和△EBF中,
$\left\{\begin{array}{l}{BG=BE}\\{∠GBF=∠EBF}\\{BF=BF}\end{array}\right.$,
∴△GBF≌△EBF(SAS),
∴EF=GF=CF+CG=CF+AE;
(3)不成立,但满足新的数量关系.
如图3,在AE上截取AH=CF,连接BH,
在△BAH和△BCF中,
$\left\{\begin{array}{l}{BA=BC}\\{∠BAH=∠BCF}\\{AH=CF}\end{array}\right.$,
∴△BAH≌△BCF(SAS),
∴BH=BF,∠ABH=∠CBF,
∵∠EBF=60°=∠FBC+∠CBE
∴∠ABH+∠CBE=60°,
∵∠ABC=120°,
∴∠HBE=60°=∠EBF,
在△EBF和△HBE中,
$\left\{\begin{array}{l}{BH=BF}\\{∠HBE=∠EBF}\\{BE=BE}\end{array}\right.$,
∴△EBF≌△EBH(SAS),
∴EF=EH,
∴AE=EH+AE=EF+CF.
点评 本题主要考查了全等三角形的判定与性质,等边三角形的判定与性质、旋转变换等知识点,难度适中.本题是典型的“大角夹半角模型”,其基本思路是“旋转补短”,从而构造全等三角形.这一类型的题目经常出现,希望同学们务必掌握.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com