
【题目】已知半径为1的⊙O中,弦AC=![]() ,弦AB=
,弦AB=![]() ,则∠CAB的度数为( )
,则∠CAB的度数为( )
A. 15° B. 60° C. 75° D. 15°或75°
【答案】D
【解析】
先根据题意画出图形,分别作AC、AB的垂线,连接OA,再根据锐角三角函数的定义求出∠OAD及∠OAE的度数,即可得出结论.
有两种情况:
①如图1,当两弦AC、AB在圆心的两侧时,过O作OD⊥AB于点D,OE⊥AC于点E,连接OA,
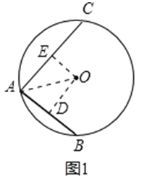
∵AB=![]() ,AC=
,AC=![]() ,
,
∴AD=![]() ,AE=
,AE=![]() ,
,
在Rt△AOD中,
∵cos∠OAD=![]() =
=![]() ,
,
∴∠OAD=45°,
在Rt△AOE中,
∵cos∠OAE=![]() =
=![]() ,
,
∴∠OAE=30°,
∴∠BAC=∠OAD+∠OAE=45°+30°=75°;
②如图2,当两弦AC、AB在圆心的同侧时,
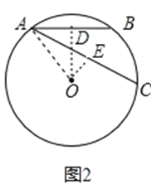
由①可知∠OAD=45°,∠OAE=30°,
∴∠BAC=∠OAD∠OAE=45°30°=15°;
综上所述,∠BAC的度数是75°或15°.
故选:D.


科目:初中数学 来源: 题型:
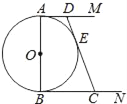
【题目】如图,⊙O的直径AB=2,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN于C.设AD=x,BC=y.
(1)求证:AM∥BN;
(2)求y关于x的关系式;
(3)求四边形ABCD的面积S,并证明:S≥2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张圆形纸片,小芳进行了如下连续操作:
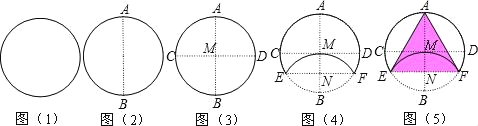
(1)将圆形纸片左右对折,折痕为AB,如图(2)所示.
(2)将圆形纸片上下折叠,使A、B两点重合,折痕CD与AB相交于M,如图(3)所示.
(3)将圆形纸片沿EF折叠,使B、M两点重合,折痕EF与AB相交于N,如图(4)所示.
(4)连结AE、AF,如图(5)所示.
经过以上操作小芳得到了以下结论:
①CD∥EF;②四边形MEBF是菱形;③△AEF为等边三角形;④![]() ,
,
以上结论正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步发展基础教育,自2016年以来,某县加大了教育经费的投入.2016年该县投入教育经费6000万元,2018年投入教育经费8640万元,假设该县这两年投入教育经费的年平均增长率相同.
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2019年该县教育经费多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 O 是△ABC 的边 AB 上一点,以 OB 为半径的⊙O 交 BC 于点 D,过点 D 的切线交 AC 于点 E,且 DE⊥AC.
(1)证明:AB=AC;
(2)设 AB=![]() cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.
cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数 y=kx+b与反比例函数 y=![]() (x>0)的图象交于A(m,6)B(3,n)两点.
(x>0)的图象交于A(m,6)B(3,n)两点.
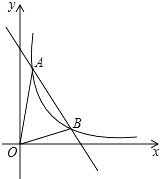
(1)求一次函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
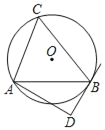
【题目】如图,⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8.AD和过点B的切线互相垂直,垂足为D.
(1)求证:∠BAD+∠C=90°;
(2)求线段AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com