
【题目】如图,抛物线y=x2+bx﹣c经过直线y=x﹣3与坐标轴的两个交点A,B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)点P为抛物线上的一个动点,求使S△APC:S△ACD=5:4的点P的坐标.

【答案】(1)y=x2﹣2x﹣3.(2)满足条件的点的坐标为(4,5)或(﹣2,5).
【解析】
(1)先根据直线y=x-3求出A、B两点的坐标,然后将它们代入抛物线中即可求出待定系数的值.
(2)根据(1)中抛物线的解析式可求出C,D两点的坐标,由于△APC和△ACD同底,因此面积比等于高的比,即P点纵坐标的绝对值:D点纵坐标的绝对值=5:4.据此可求出P点的纵坐标,然后将其代入抛物线的解析式中,即可求出P点的坐标.
(1)直线y=x-3与坐标轴的交点A(3,0),B(0,-3).
则![]() ,
,
解得![]() ,
,
∴此抛物线的解析式y=x2-2x-3.
(2)抛物线的顶点D(1,-4),与x轴的另一个交点C(-1,0).
设P(a,a2-2a-3),则(![]() ×4×|a2-2a-3|):(
×4×|a2-2a-3|):(![]() ×4×4)=5:4.
×4×4)=5:4.
化简得|a2-2a-3|=5.
当a2-2a-3=5,得a=4或a=-2.
∴P(4,5)或P(-2,5),
当a2-2a-3<0时,即a2-2a+2=0,此方程无解.
综上所述,满足条件的点的坐标为(4,5)或(-2,5).


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
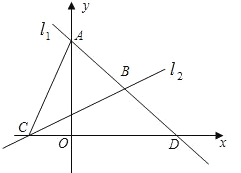
【题目】如图,直线l1过点A(0,4),点D(4,0),直线l2:![]() 与x轴交于点C,两直线
与x轴交于点C,两直线![]() ,
,![]() 相交于点B.
相交于点B.
(1)求直线![]() 的解析式和点B的坐标;
的解析式和点B的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小杰在学完了《锐角三角比》知识后回家整理笔记,写下了下列四句活:(1)锐角A的正弦的值的范围是0<sinA<1;(2)根据正切和余切的意义,可以得到tanA=![]() ;(3)在Rt△ABC中,如∠C=90°,则cosB=sinA;(4)在Rt△ABC中,如∠C=90°,则cotB=tanA;请你判断上述语句正确的个数是( )
;(3)在Rt△ABC中,如∠C=90°,则cosB=sinA;(4)在Rt△ABC中,如∠C=90°,则cotB=tanA;请你判断上述语句正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
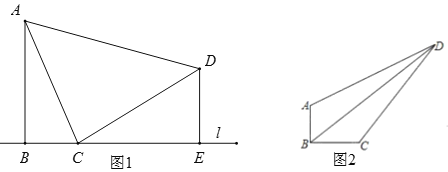
【题目】(1)如图1,已知AB⊥l,DE⊥l,垂足分别为B、E,且C是l上一点,∠ACD=90°.求证:△ABC∽△CED;
(2)如图2,在四边形ABCD中,∠ABC=90°,AB=6,BC=8,CD=20,DA=![]() .求BD的长为_______.
.求BD的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次函数![]() ≠0
≠0![]() 的图像经过点(3,5)、(2,8)、(0,8).
的图像经过点(3,5)、(2,8)、(0,8).
①求这个二次函数的解析式;
②已知抛物线![]() ≠0
≠0![]() ,
,![]() ≠0
≠0![]() ,且满足
,且满足![]() ≠0,1
≠0,1![]() ,则我们称抛物线
,则我们称抛物线![]() 互为“友好抛物线”,请写出当
互为“友好抛物线”,请写出当![]() 时第①小题中的抛物线的友好抛物线,并求出这“友好抛物线”的顶点坐标.
时第①小题中的抛物线的友好抛物线,并求出这“友好抛物线”的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
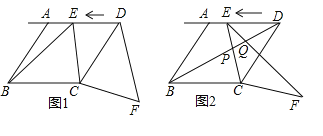
【题目】如图1,在菱形ABCD中,AB=6![]() ,tan∠ABC=2,点E是射线DA上的一个动点,连接CE,将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.
,tan∠ABC=2,点E是射线DA上的一个动点,连接CE,将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.
(1)求证:△BCE≌△DCF;
(2)求线段DF的长度的最小值;
(3)如图2,连接BD、EF.BD交EC、EF于点P、Q.当△EPQ是直角三角形时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P、Q分别从点A、B同时开始移动,点P的速度为1 cm/秒,点Q的速度为2 cm/秒,点Q移动到点C后停止,点P也随之停止运动下列时间瞬间中,能使△PBQ的面积为15cm 的是( )
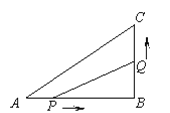
A. 2秒钟 B. 3秒钟 C. 4秒钟 D. 5秒钟
查看答案和解析>>
科目:初中数学 来源: 题型:
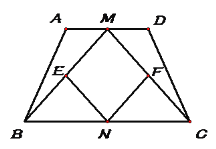
【题目】如图,在等腰梯形ABCD中,AB=DC,点M,N分别是AD,BC的中点,点E,F分别是BM,CM的中点. (1)求证:四边形MENF是菱形; (2)当四边形MENF是正方形时,求证:等腰梯形ABCD的高是底边BC的一半.
查看答案和解析>>
科目:初中数学 来源: 题型:
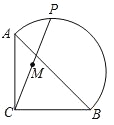
【题目】如图,在等腰 Rt△ABC 中,AC=BC= 2![]() ,点 P 在以斜边 AB 为直径的半圆上,M 为 PC的中点.当点 P 沿半圆从点 A 运动至点 B 时,点 M 运动的路径长是( )
,点 P 在以斜边 AB 为直径的半圆上,M 为 PC的中点.当点 P 沿半圆从点 A 运动至点 B 时,点 M 运动的路径长是( )
A. 2 B. 2 ![]() C. π D.
C. π D. ![]() π
π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com