
����Ŀ����1����ͼ1����֪������ABC�У�AB=AC=10��BDƽ����ABC��CDƽ����ACB������D��EF��BC���ֱ�AB��AC��E��F���㣬��ͼ�й���__________�����������Σ�EF��BE��CF֮���������ϵ��__________����AEF���ܳ���__________��
��2����ͼ2��������1��������ABC�У�AB=AC=10����Ϊ������ABCΪ���ȱ������Σ�AB=8��AC=10�������������䣬��ͼ�й���__________�����������Σ�EF��BE��CF֮���������ϵ��ʲô��֤����Ľ��ۣ��������AEF���ܳ���
��3����֪����ͼ3��D����ABC�⣬AB>AC����BDƽ����ABC��CDƽ����ABC�������ACG������D��DE��BC���ֱ�AB��AC��E��F���㣬��EF��BE��CF֮�����к�������ϵ�أ�ֱ��д�����۲�֤����

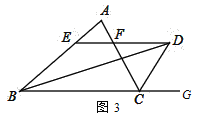
���𰸡���1��5��BE+CF=EF��20�� ��2��2��BE+CF=EF��֤������������AEF���ܳ�=18����3��BE-CF=EF�����ɼ�����.
�������������������1�����ݽ�ƽ���ߵĶ���ɵ���EBD=��CBD����FCD=��BCD���ٸ�����ֱ��ƽ�У��ڴ�����ȿɵ���EDB=��CBD����FDC=��BCD��Ȼ�������EBD=��EDB����FDC=��BCD���ٸ��ݵȽǶԵȱ߿ɵ�BE=DE��CF=DF��Ȼ���ɣ�
��2�����ݽ�ƽ���ߵĶ���ɵ���EBD=��CBD����FCD=��BCD���ٸ�����ֱ��ƽ�У��ڴ�����ȿɵ���EDB=��CBD����FDC=��BCD��Ȼ�������EBD=��EDB����FDC=��BCD���ٸ��ݵȽǶԵȱ߿ɵ�BE=DE��CF=DF��Ȼ���ɣ�
��3���ɣ�2��֪BE=ED��CF=DF��Ȼ�����õ�����������֤��BE��CF��EF��������������ϵ��
����������⣺��1��BE+CF=EF���������£�
��AB=AC�����ABC=��ACB����BDƽ����ABC��CDƽ����ACB�����EBD=��CBD����FCD=��BCD�����DBC=��DCB����DB=DC��
��EF��BC�����AEF=��ABC����AFE=��ACB����EDB=��CBD����FDC=��BCD�����EBD=��EDB����FDC=��BCD����BE=DE��CF=DF��AE=AF������������������ABC����AEF����DEB����DFC����BDC��5������BE+CF=DE+DF=EF����BE+CF=EF����AEF���ܳ�=AE+EF+AF=AE+BE+AF+FC=AB+AC=20��
�ʴ�Ϊ��5��BE+CF=EF��20��
��2��BE+CF=EF����BDƽ����ABC��CDƽ����ACB�����EBD=��CBD����FCD=��BCD����EF��BC�����EDB=��CBD����FDC=��BCD�����EBD=��EDB����FDC=��BCD����BE=DE��CF=DF������������������BDE����CFD����BE+CF=DE+DF=EF����BE+CF=EF����AEF���ܳ�=AE+EF+AF=AE+ED+DF+AF=AE+EB+CF+AF=AB+AC=8+10=18��
��ʱ���������������Σ�EF��BE��CF��C��AEF��18��
��3��BE��CF=EF���ɣ�1��֪BE=ED����EF��BC�����EDC=��DCG=��ACD����CF=DF������ED��DF=EF����BE��CF=EF��


 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��1��0����B��11��0������CΪ�߶�AB��һ���㣬��ACΪֱ���ġ�D�İ뾶DE��AC����CBF����CBΪб�ߵĵ���ֱ�������Σ��ҵ�E��F���ڵ������ޣ�����F������A��C��E����������ߵĶ���ľ�����Сʱ���������ߵĽ���ʽΪ 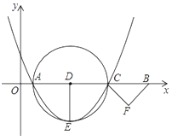
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
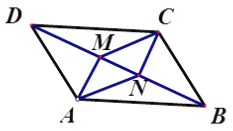
����Ŀ����ͼ����ƽ���ı���ABCD�У�AM��CN����BD�Ĵ��ߣ�M��N�Ǵ��㣮
��֤����1��AM=CN����2����MAN=��NCM��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪OΪֱ��AB��һ�㣬��COE��ֱ�ǣ�OFƽ�֡�AOE.
(1)��ͼ�٣�����COF��34�㣬���BOE��________������COF��n�㣬���BOE��________����BOE���COF��������ϵΪ________________��
(2)������OE�Ƶ�O��ʱ����ת����ͼ�ڵ�λ��ʱ��(1)�С�BOE���COF��������ϵ�Ƿ���Ȼ��������˵�����ɣ�
(3)��ͼ���У�����COF��65�㣬�ڡ�BOE���ڲ��Ƿ����һ������OD��ʹ��2��BOD���AOF�ĺ͵��ڡ�BOE���BOD�IJ��һ�룿�����ڣ��������BOD�Ķ������������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
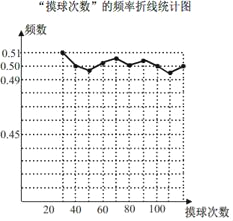
����Ŀ����һ������������װ����ɫ��ͬ�ĺڡ���������40����Сӱ������ʵ�飬�����������������Ⱥ�����������һ���������ɫ���ٰ����Żغ����У������ظ��������̣���ͼ����������������Ƶ������ͳ��ͼ��
��1������ͳ��ͼ�����������ڡ���������ɫ��������ٸ���
��2�����Ҫʹ��������ĸ���Ϊ![]() ����Ҫ���������ٷ�����ٸ�����
����Ҫ���������ٷ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�AB��������Ҫ����ɻ�ͼ�ͼ��㣺
(1)�ӳ��߶�AB����C��ʹBC��2AB��ȡAC�е�D��
(2)��(1)�������£����AB��4�����߶�BD�ij��ȣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABCD�У�BE��CE�ֱ�ƽ����ABC����BCD��E��AD�ϣ�BE=12cm��CE=5cm����ABCD���ܳ��������
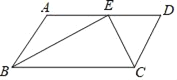
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��г��۸�30Ԫ/ǧ���չ���һ������1000ǧ�˴����������Ԥ�⣬���ʵ��г��۸�ÿ��ÿǧ������1Ԫ���䶳�����������ÿ����Ҫ֧�����ַ��úϼ�310Ԫ��������Щ����������������160�죬ͬʱƽ��ÿ����3ǧ�˵ĺ��ʱ��ʣ�
��1����x���ÿǧ�˸ú��ʵ��г��۸�ΪyԪ����д��y��x֮��ĺ�����ϵʽ��
��2�������x�����������һ���Գ��ۣ����������ʵ������ܶ�ΪPԪ����д��P��x֮��ĺ�����ϵʽ��
��3��С��������ʴ�Ŷ��������ۿɻ�����������������Ƕ���Ԫ��������W=�����ܶ�չ��ɱ������ַ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�CD�DZ�AB�ϵĸߣ���![]() =
=![]() ��
��
��1����֤����ACD�ס�CBD��
��2�����ACB�Ĵ�С��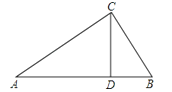
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com