
【题目】如图,线段MN是周长为36cm的圆的直径(圆心为O),动点A从点M出发,以![]() 的速度沿顺时针方向在圆周上运动,经过点N时,其速度变为
的速度沿顺时针方向在圆周上运动,经过点N时,其速度变为![]() ,并以这个速度继续沿顺时针方向运动之点M后停止。在动点A运动的同时,动点B从点N出发,以
,并以这个速度继续沿顺时针方向运动之点M后停止。在动点A运动的同时,动点B从点N出发,以![]() 的速度沿逆时针方向在圆周上运动,绕一周后停止运动。设点A、点B运动时间为
的速度沿逆时针方向在圆周上运动,绕一周后停止运动。设点A、点B运动时间为![]() .
.
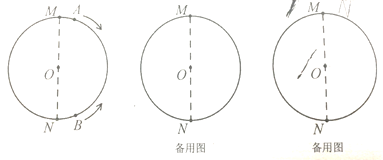
(1)连接OA、OB,当t=4时,![]() = °,在整个运动过程中,当
= °,在整个运动过程中,当![]() 时,点A运动的路程为 cm(第2空结果用含t的式子表示);
时,点A运动的路程为 cm(第2空结果用含t的式子表示);
(2)当A、B两点相遇时,求运动时间t;
(3)连接OA、OB,当![]() 时,请直接写出所有符合条件的运动时间t.
时,请直接写出所有符合条件的运动时间t.
【答案】(1)20;![]() ;(2)当A、B两点相遇时,t=
;(2)当A、B两点相遇时,t=![]() 或
或![]() ;(3)当
;(3)当![]() 时,t=3或
时,t=3或![]() 或12或
或12或![]()
【解析】
(1)根据圆O的周长,即可求出半圆![]() 的长,然后求出当t=4时,点A的运动路程
的长,然后求出当t=4时,点A的运动路程![]() 和点B的运动路程
和点B的运动路程![]() ,即可求出
,即可求出![]() ,然后求出
,然后求出![]() 占圆周长的分率乘360°即可求出
占圆周长的分率乘360°即可求出![]() ,画出
,画出![]() ,根据点A行驶的路程
,根据点A行驶的路程![]() =半圆
=半圆![]() +
+![]() 和速度即可求出结论;
和速度即可求出结论;
(2)根据第一次相遇和第二次相遇分类讨论,分别画出对应的图形,然后根据图形找出等量关系即可求出t的值;
(3)根据第一次相遇前![]() 、第一次相遇后
、第一次相遇后![]() 、第二次相遇前
、第二次相遇前![]() 、第二次相遇后
、第二次相遇后![]() ,分类讨论分别画出对应的图形,然后根据图形找出等量关系即可求出t的值.
,分类讨论分别画出对应的图形,然后根据图形找出等量关系即可求出t的值.
解:(1)∵圆O的周长为36cm
∴半圆![]() 的长为36÷2=18cm
的长为36÷2=18cm
当t=4时,根据题意可得![]() =3×4=12cm,
=3×4=12cm,![]() =2×4=8cm,如下图所示
=2×4=8cm,如下图所示

∴![]() =
=![]() +
+![]() -半圆
-半圆![]() =2cm
=2cm
∴∠AOB=![]()
点A到点N所需时间为18÷3=6s
当![]() 时,如下图所示
时,如下图所示

点A行驶的路程![]() =半圆
=半圆![]() +
+![]() =18+
=18+![]() =
=![]()
故答案为:20;![]() .
.
(2)当A、B两点第一次相遇时,如下图所示:
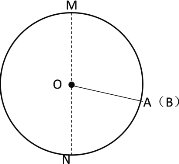
此时![]() +
+![]() =半圆
=半圆![]()
∴3t+2t=18
解得:t=![]() ;
;
当A、B两点第二次相遇时,如下图所示:

此时![]() +
+![]() -半圆
-半圆![]() =圆O的周长
=圆O的周长
即![]() +2t-18=36
+2t-18=36
解得:t=![]()
综上所述:当A、B两点相遇时,t=![]() 或
或![]() ;
;
(3)①当点A、B第一次相遇之前,∠AOB=30°时,如下图所示

此时![]() +
+![]() +
+![]() =半圆
=半圆![]()
即3t+![]() +2t=18
+2t=18
解得:t=3;
②当点A、B第一次相遇之后,∠AOB=30°时,如下图所示

此时![]() -
-![]() +
+![]() =半圆
=半圆![]()
即3t-![]() +2t=18
+2t=18
解得:t=![]() ;
;
③当点A、B第二次相遇之前,∠AOB=30°时,如下图所示
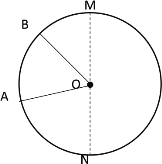
此时![]() +
+![]() -半圆
-半圆![]() +
+![]() =圆O的周长
=圆O的周长
即![]() +2t-18+
+2t-18+![]() =36
=36
解得:t=12;
④当点A、B第二次相遇之后,∠AOB=30°时,如下图所示
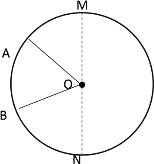
此时![]() +
+![]() -半圆
-半圆![]() -
-![]() =圆O的周长
=圆O的周长
即![]() +2t-18-
+2t-18-![]() =36
=36
解得:t=![]() ;
;
综上所述:当![]() 时,t=3或
时,t=3或![]() 或12或
或12或![]() .
.


科目:初中数学 来源: 题型:
【题目】在推进城乡义务教育均衡发展工作中,我市某区政府通过公开招标的方式为辖区内全部乡镇中学采购了某型号的学生用电脑和教师用笔记本电脑,其中,A乡镇中学更新学生用电脑110台和教师用笔记本电脑32台,共花费30.5万元;B乡镇中学更新学生电脑55台和教师用笔记本电脑24台,共花费17.65万元.
(1)求该型号的学生用电脑和教师用笔记本电脑单价分别是多少万元?
(2)经统计,全部乡镇中学需要购进的教师用笔记本电脑台数比购进的学生用电脑台数的![]() 少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台?
少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 .在数轴.上有![]() 两个点(点
两个点(点![]() 在点
在点![]() 的左侧) ,
的左侧) , ![]()
![]()
(1)如果点![]() 表示的数是
表示的数是![]() ,那么,
,那么,
①点![]() 表示的数是_______.
表示的数是_______.
②如果点![]() 从点
从点![]() 出发,沿数轴正方向运动,速度是每秒3个单位长度,运动秒后,点
出发,沿数轴正方向运动,速度是每秒3个单位长度,运动秒后,点![]() 表示的数是_______.( 用含
表示的数是_______.( 用含![]() 的代数式表示) ; 经过________秒 ,
的代数式表示) ; 经过________秒 , ![]() .
.
(2)如果点![]() 表示的数是
表示的数是![]() ,将数轴的负半轴绕原点
,将数轴的负半轴绕原点![]() 顺时针旋转60° ,得到
顺时针旋转60° ,得到![]() ,如图2所示,射线
,如图2所示,射线![]() 从
从![]() 出发绕点
出发绕点![]() 顺时针旋转,速度是每秒15° ,同时,射线
顺时针旋转,速度是每秒15° ,同时,射线![]() 从
从![]() 出发绕点
出发绕点![]() 逆时针旋转,速度是每秒5° .设运动时间为
逆时针旋转,速度是每秒5° .设运动时间为![]() 秒,当
秒,当![]() 秒时,
秒时, ![]() 停止运动.
停止运动.
①当![]() 为________秒时,
为________秒时,![]() 与
与![]() 重合.
重合.
②当![]() 时,
时,![]() 的值是________.
的值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AEAD=AHAF;其中结论正确的个数是( )
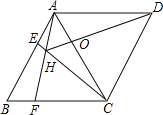
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生到相距80km的江阴黄山湖公园进行社会实践活动.上午8:00学生乘长途汽车从学校出发.上午8:30一位老师带着两名迟到的学生乘小轿车从学校出发,结果小轿车比长途汽车晚10分钟到达目的地.
(1)小汽车的行驶时间比长途汽车的行驶时间少 小时;(请直接写出答案)
(2)已知小轿车的平均速度是长途汽车的1.5倍,求小轿车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=ax2+bx﹣4(a≠0)的图象与x轴交于A(﹣2,0)、C(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
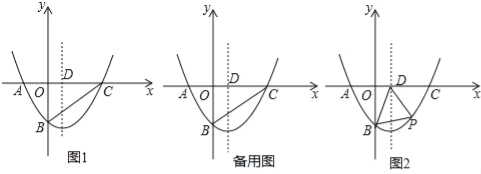
(1)求该二次函数的解析式;
(2)如图1,连结BC,在线段BC上是否存在点E,使得△CDE为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)如图2,若点P(m,n)是该二次函数图象上的一个动点(其中m>0,n<0),连结PB,PD,BD,求△BDP面积的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,按下列方法将数轴的正半轴绕在一个圆上(该圆周长为![]() 个单位长,且在圆周的三等分点处分别标上了数字
个单位长,且在圆周的三等分点处分别标上了数字![]() ,
,![]() ,
,![]() )上:先让原点与圆周上
)上:先让原点与圆周上![]() 所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上
所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 所对应的点分别与圆周上
所对应的点分别与圆周上![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 所对应的点重合,这样,正半轴上的整数就与圆周上的数字建立了一种对应关系.
所对应的点重合,这样,正半轴上的整数就与圆周上的数字建立了一种对应关系.
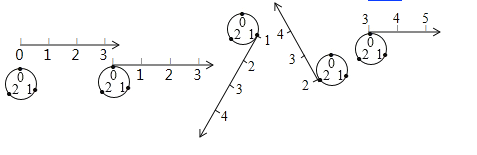
(1)圆周上数字![]() 与数轴上的数
与数轴上的数![]() 对应,则
对应,则![]() __________.
__________.
(2)数轴上的一个整数点刚刚绕过圆周![]() 圈(
圈(![]() 为正整数)后,并落在圆周上数字
为正整数)后,并落在圆周上数字![]() 所对应的位置,这个整数是____________.(用含
所对应的位置,这个整数是____________.(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y=![]() 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
(1)危险检测表在气体泄漏之初显示的数据是 ;
(2)求反比例函数y=![]() 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面文字后,解答问题
有这样一道题目:“已知:二次函数![]() 的图象经过点(1,0)_________,
的图象经过点(1,0)_________,
求证:这个二次函数图象关于直线![]() 对称”
对称”
题目中的横线部分是一段被墨水污染了无法辨认的文字.
根据现有信息,题目中二次函数图象不具有的性质是( )
A. 过点(3,0) B. 顶点是(2,-2)
C. 在X轴上截得的线段长是2 D. 与Y轴交点是(0,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com