
����Ŀ�������龳��
���ۺ���ʵ�����ϣ���ʦ��ͬѧ���ԡ�����ֽƬ�ļ�ƴ��Ϊ���չ��ѧ����� ͼ 1����������ֽƬ ABCD �ضԽ��� AC �������õ���ABC �͡�ACD���������� AB ��4cm��AC��8cm��
�������֣�
��1����ͼ 1 �еġ�ACD �Ե� A Ϊ��ת���ģ�����ʱ�뷽����ת�Ϧ���ʹ�Ϧ�����BAC���õ���ͼ 2 ��ʾ�ġ�AC��D������ C �� AC���ƽ���ߣ��� DC'���ӳ��� ���ڵ� E�����ı��� ACEC�����״�� ��
��2������С�齫ͼ 1 �еġ�ACD �Ե� A Ϊ��ת���ģ�����ʱ�뷽����ת��ʹ B�� A��D ������ͬһ��ֱ���ϣ��õ���ͼ 3 ��ʾ�ġ�AC��D������ CC'��ȡ CC����� �� F������ AF ���ӳ����� G��ʹ FG��AF������ CG��C��G���õ��ı��� ACGC�䣬 �������������Σ�����֤��������ۣ�
ʵ��̽����
��3������С���ڴ���С�鷢�ֽ��۵Ļ����ϣ��������²���������ABC ���� BD ����ƽ�ƣ�ʹ�� B ��� A �غϣ���ʱ A ��ƽ���� A'�㣬A'C �� BC���ཻ�ڵ� H�� ��ͼ 4 ��ʾ������ CC�䣬���� tan��C��CH ��ֵ��
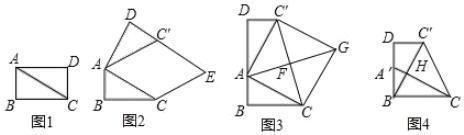
���𰸡���1�����Σ���2������������3��tan��C��CH��![]() ��
��
��������
��1������![]() ���Եõ�
���Եõ�![]() ,�ٽ��
,�ٽ��![]() ���Եõ�
���Եõ�![]() ,����֪
,����֪![]() ���Եõ��ı���
���Եõ��ı���![]() Ϊƽ���ı��Σ�������ת������
Ϊƽ���ı��Σ�������ת������![]() ,�Ӷ��õ��ı���
,�Ӷ��õ��ı���![]() Ϊ���Σ�
����
��2������![]() ���Եõ��ı���
���Եõ��ı���![]() Ϊƽ���ı��Σ���
Ϊƽ���ı��Σ���![]() �������ı���
�������ı���![]() Ϊ����,��ôֻ��Ҫ��֤��һ��ֱ�Ǽ��ɣ���
Ϊ����,��ôֻ��Ҫ��֤��һ��ֱ�Ǽ��ɣ���![]() ��
��![]() ��
��![]() ���㹲��ʱ:
���㹲��ʱ:![]() ����������ת�����ʣ�
����������ת�����ʣ�![]() ,���Եõ���
,���Եõ���
![]() ,�Ӷ�֤���ı���
,�Ӷ�֤���ı���![]() Ϊ�����Σ�
������
��3����ϵڶ��ʿ��Եõ�![]() ,����Ҫ��
,����Ҫ��![]() ���Ϳ��Էֱ����
���Ϳ��Էֱ����![]() ��
��![]() �ó��ȣ���������Եõ�
�ó��ȣ���������Եõ�![]() ,��ô
,��ô![]() ��������Ǻ����ֱ�Ϳ��Էֱ����
��������Ǻ����ֱ�Ϳ��Էֱ����![]() ��
��![]() ��
��
��1�����Σ��������£�
����ת�����ʿɵã�![]()
![]()
![]()
![]() ����
����![]()
��![]()
![]()
![]()
![]()
![]() �ı���
�ı���![]() Ϊƽ���ı���
Ϊƽ���ı���
����ת�����ʿɵã�![]()
![]() �ı���
�ı���![]() Ϊ���Σ�
����
��2�������Σ��������£�
![]()
![]()
![]() �ı���
�ı���![]() Ϊƽ���ı���
Ϊƽ���ı���
��![]()
![]()
![]() �ı���
�ı���![]() Ϊ����
����
��![]() ��
��![]() ��
��![]() ���㹲��ʱ:
���㹲��ʱ:![]()
����ת�����ʵã�![]()
![]()
![]()
![]() �ı���
�ı���![]() Ϊ�����Σ�
������
��3����![]() ��AB��4��AC��8��
��AB��4��AC��8��
![]()
![]()
![]()
![]()
![]()
�ɣ�2�����ƽ��֪��![]()
��![]() ��
�У�![]()
![]()
![]()
![]()
![]()
��![]() ��
�У�![]() ;
;



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
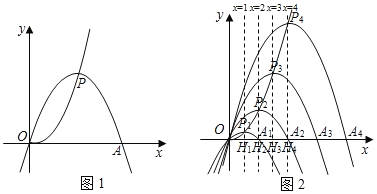
����Ŀ����֪��PΪ������y![]() x2��һ���㣬��PΪ���㣬�Ҿ���ԭ��O�������ߣ�������yp����������x����һ����ΪA����P�ĺ�����Ϊm��
x2��һ���㣬��PΪ���㣬�Ҿ���ԭ��O�������ߣ�������yp����������x����һ����ΪA����P�ĺ�����Ϊm��
��1��������OPAΪֱ��������ʱ��m=����������
������OPAΪ�ȱ�������ʱ�����ʱ��yp���Ľ���ʽ��
��2����P��ĺ�����ֱ�Ϊ1��2��3����n(nΪ������)ʱ�������ߡ�yp���ֱ������![]() ������
������![]() ��������
��������![]() ����������x������һ����ֱ�ΪA1��A2��A3����An����P1��P2��P3����Pn��x��Ĵ��ߣ�����ֱ�ΪH1��H2��H3����Hn��
����������x������һ����ֱ�ΪA1��A2��A3����An����P1��P2��P3����Pn��x��Ĵ��ߣ�����ֱ�ΪH1��H2��H3����Hn��
��1)�� Pn������Ϊ����������OAn=����������(�ú�n�Ĵ���ʽ����ʾ)
����PnHn��OAn=16ʱ����n��ֵ��
��2)�Ƿ����������An��ʹ�á�OP4An=90�㣬�����ڣ���n��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���¹ڷ���������ȫ�����ӣ���������ص���Ա�����;�����ʧ������һ��ԭ�����¹ڷ��ײ��������ٶȷdz��죮һ���������Ⱦij�ֲ��������������ֵĴ�����Ⱦ�����������ﵽ64�ˣ�
��1�������ֲ���ÿ�ִ�����һ����ƽ����Ⱦ�����ˣ�
��2����������Ĵ����ٶȣ���������ò������ƣ��������ִ�����һ���ж����˱���Ⱦ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
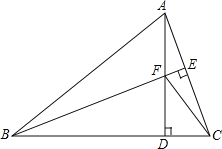
����Ŀ����ͼ���ڡ�ABC�У�AB=BC��BE��AC�ڵ�E��AD��BC�ڵ�D����BAD=45����CD=![]() ��AD��BE���ڵ�F������CF����AD�ij�Ϊ_____��
��AD��BE���ڵ�F������CF����AD�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
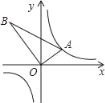
����Ŀ����ͼ����AOB��ֱ�������Σ���AOB��90����OB��2OA����A�ڷ���������y��![]() ��ͼ���ϣ�����B�ڷ���������y��
��ͼ���ϣ�����B�ڷ���������y��![]() ��ͼ���ϣ���k��ֵΪ_____��
��ͼ���ϣ���k��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
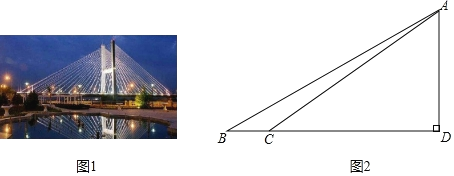
����Ŀ����ͼ��һ���ִ������͵���˫������б���ţ����Ų��ö���˫����б����ƣ������ʡ�H���Σ������ø�˿��б���̶���
���������
��β�����������������ľ���AD��
������ƣ�
��ͼ��ij��ѧ�����о�С��ͨ�������о���ʵ�ز�����������B����á�ABC=26.57�㣬����BD������21����C������C����á�ACD=30.96�㣮
��������
�����������������ݣ�����̲�ƺӴ�����������������ľ���AD��
(�����ȷ��1m���ο����ݣ�sin26.57���0.447��cos26.57���0.894��tan26.57���0.500��sin30.96���0.514��cos30.96���0.858��tan30.96���0.600)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC��ƽ��ֱ������ϵ�е�λ����ͼ������ÿ��С�����εı߳�Ϊ1����λ���ȣ�
(1)������ABC����ԭ��O�����ĶԳ�ͼ�Ρ�A1B1C1��
(2)��������ABC�Ƶ�C˳ʱ����ת90���õ���A2B2C2��
(3)��(2)�������£����A��ת����A2��������·�߳�(���������)��
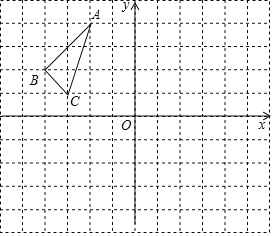
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
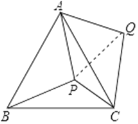
����Ŀ��P�ǵȱ���ABC�ڲ�һ�㣬��APB����BPC����CPA�Ĵ�С֮����5��6��7������ABP��ʱ����ת��ʹ��AB��AC�غϣ�����PA��PB��PC�ij�Ϊ�ߵ������ε������ǡ�PCQ����QPC����PQC=________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
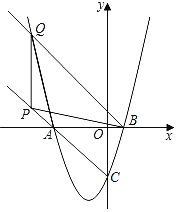
����Ŀ����ͼ��������y��x2��ax+a��1��x�ύ��A��B���㣨��B���������ϣ�����y�ύ�ڵ�C��OA��3OB����P��CA���ӳ����ϣ���Q�ڵڶ������������ϣ�S��PBQ��S��ABQ��
��1���������ߵĽ���ʽ��
��2����ֱ��BQ�Ľ���ʽ��
��3������PAQ����APB�����P�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com