
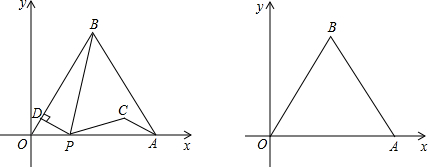
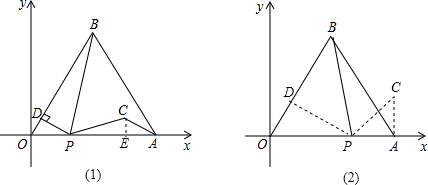
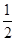 OP.∵OP=t,∴OD=
OP.∵OP=t,∴OD=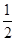 t,在Rt△OPD中,由勾股定理,得PD=
t,在Rt△OPD中,由勾股定理,得PD=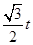
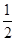 t,∴BD=4-
t,∴BD=4-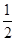 t.
t.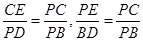
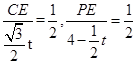 ,,
,,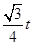 ,PE=
,PE=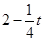 ,OE=
,OE=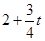 ,∴C(
,∴C(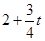 ,
,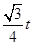 ).
).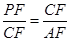 ,∴CF2=PF•AF,
,∴CF2=PF•AF,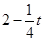 ,AF=4-OF=2-
,AF=4-OF=2-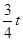 CF=
CF=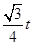 ,
,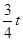 )2=(
)2=(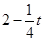 )(2-
)(2-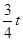
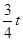 ),
),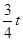 =4∴t=
=4∴t=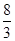
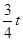 ,y=
,y=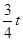 ,∴y=
,∴y=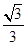 x-
x-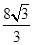 ,
,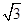 ),∴由两点间的距离公式得:C1C2=2
),∴由两点间的距离公式得:C1C2=2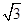 .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
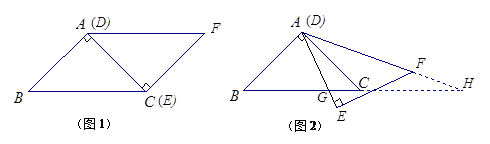
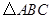 ,以
,以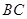 为直径,
为直径,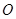 为圆心的半圆交
为圆心的半圆交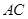 于点
于点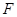 ,点
,点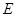 为弧CF的中点,连接
为弧CF的中点,连接 交
交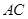 于点
于点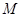 ,
,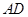 为△ABC的角平分线,且
为△ABC的角平分线,且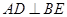 ,垂足为点
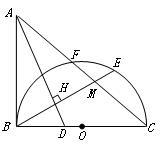
,垂足为点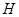 .
.
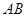 是半圆
是半圆 的切线;
的切线;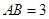 ,
,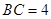 ,求
,求 的长.
的长.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
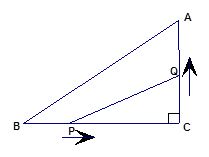
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com