
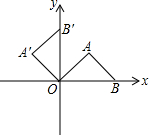
 将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为
将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为
| ||
| 2 |
| 2 |
| 2 |
| ||
| 2 |
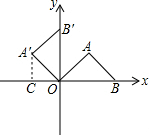 解:作A′C⊥x轴于C,如图,
解:作A′C⊥x轴于C,如图,
| ||
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |


科目:初中数学 来源: 题型:
| k | x |

查看答案和解析>>
科目:初中数学 来源:活学巧练九年级数学上 题型:044
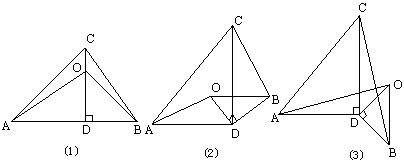
如图(1),A,D,B三点在同一直线上,△ACD,△BOD均为等腰直角三角形,即∠ADC=∠BDO=![]() ,试猜想AO,BC有何关系,并证明你的结论,若将△ODB绕顶点D旋转到图(2)、图(3)的位置,上述关系是否仍然成立?若成立,则它表明了几何学中的一个基本事实是________(在横线上填出来),若不成立,请简要说明理由.
,试猜想AO,BC有何关系,并证明你的结论,若将△ODB绕顶点D旋转到图(2)、图(3)的位置,上述关系是否仍然成立?若成立,则它表明了几何学中的一个基本事实是________(在横线上填出来),若不成立,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (x>0)也恰好经过点A.
(x>0)也恰好经过点A.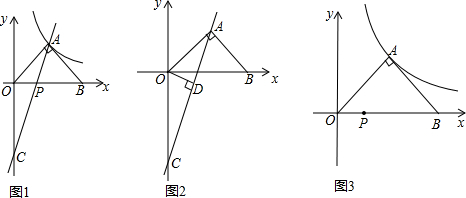
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏泰兴实验初级中学八年级上期末考试数学试卷(带解析) 题型:解答题
已知,平面直角坐标系中,矩形OABC的边OC在x轴正半轴上,边OA在y轴正半轴上,B点的坐标为(4,3).将△AOC沿对角线AC所在的直线翻折,得到△AO’C,点O’为点O的对称点,CO’与AB相交于点E(如图①).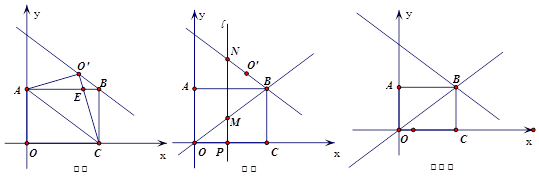
(1)试说明:EA=EC;
(2)求直线BO’的解析式;
(3)作直线OB(如图②),直线l平行于y轴,分别交x轴、直线OB、O’B于点P、M、N,设P点的横坐标为m(m>0).y轴上是否存在点F,使得ΔFMN为等腰直角三角形?若存在,请求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏泰兴实验初级中学八年级上期末考试数学试卷(解析版) 题型:解答题
已知,平面直角坐标系中,矩形OABC的边OC在x轴正半轴上,边OA在y轴正半轴上,B点的坐标为(4,3).将△AOC沿对角线AC所在的直线翻折,得到△AO’C,点O’为点O的对称点,CO’与AB相交于点E(如图①).

(1)试说明:EA=EC;
(2)求直线BO’的解析式;
(3)作直线OB(如图②),直线l平行于y轴,分别交x轴、直线OB、O’B于点P、M、N,设P点的横坐标为m(m>0).y轴上是否存在点F,使得ΔFMN为等腰直角三角形?若存在,请求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com