
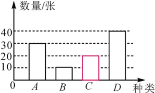
【题目】暑假期间,为激发同学们的学习热情,王华所在的学校组织全校三好学生分别到A,B,C,D四所全国重点学校参观(每个学生只能去一处),王华很高兴她也能够前往,学校按定额购买了前往四地的车票.如图是未制作完成的车票种类和数量的条形统计图和扇形统计图.请根据以上信息回答:

(1)本次参加参观的学生有 人,将条形统计图补充完整;
(2)若学校采用随机抽取的方式分发车票,每人一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么王华抽到去B地的概率是多少?
(3)已知A,B,C三地车票的价格如下表,去D地花费的车票总款数占全部车票总款数的![]() ,试求D地每张车票的价格.
,试求D地每张车票的价格.
地点 | 票价(元/张) |
A | 60 |
B | 80 |
C | 50 |
【答案】(1)100,补图见解析;(2)![]() ;(3)D地每张车票的价格为40元
;(3)D地每张车票的价格为40元
【解析】
(1)用D的人数除以D的百分比即可得出总人数;再用总人数减去A、B和D的人数即可得出C的人数;
(2)用B的人数除以总人数即可得出答案;
(3)设出去D地的车票价格,根据“去D地花费的车票总款数占全部车票总款数的![]() ”列出方程,解方程即可得出答案.
”列出方程,解方程即可得出答案.
解:(1)本次参加参观的学生有40÷40%=100(人)
去C地的人数为100-30-10-40=20(人)
条形统计图补充如图.
(2)P=![]() =
=![]() .
.
(3)设D地每张车票的价格为x元,根据题意得
![]() (60×30+80×10+50×20+40x)= 40x,
(60×30+80×10+50×20+40x)= 40x,
解得x =40.
答:D地每张车票的价格为40元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)-(3)题.
数学课上,老师出示了这样一道题:
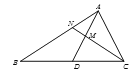
如图,△ABC中,D为BC中点,且AD=AC,M为AD中点,连结CM并延长交AB于N.
探究线段AN、MN、CN之间的数量关系,并证明.
同学们经过思考后,交流了自已的想法:
小明:“通过观察和度量,发现线段AN、AB之间存在某种数量关系.”
小强:“通过倍长不同的中线,可以得到不同的结论,但都是正确的,大家就大胆的探究吧.”
小伟:“通过构造、证明相似三角形、全等三角形,就可以将问题解决.”
......
老师: “若其他条件不变,设AB=a,则可以用含a的式子表示出线段CM的长.”
(1)探究线段AN、AB之间的数量关系,并证明;
(2)探究线段AN、MN、CN之间的数量关系,并证明;
(3)设AB=a,求线段CM的长(用含a的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过点A(1,2)和B(0,-1)且对称轴为x2.
(1)求这个二次函数的解析式;
(2)抛物线上点P(2,m)在图象上,求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
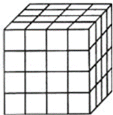
【题目】如图,把一个木制正方体的表面涂上颜色,然后将正方体分割成64个大小相同的小正方体.从这些小正方体中任意取出一个,求取出的小正方体:
(1)三面涂有颜色的概率;
(2)两面涂有颜色的概率;
(3)各个面都没有颜色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L1:y=﹣x2+bx+c经过点A(1,0)和点B(5,0)已知直线l的解析式为y=kx﹣5.
(1)求抛物线L1的解析式、对称轴和顶点坐标.
(2)若直线l将线段AB分成1:3两部分,求k的值;
(3)当k=2时,直线与抛物线交于M、N两点,点P是抛物线位于直线上方的一点,当△PMN面积最大时,求P点坐标,并求面积的最大值.
(4)将抛物线L1在x轴上方的部分沿x轴折叠到x轴下方,将这部分图象与原抛物线剩余的部分组成的新图象记为L2
①直接写出y随x的增大而增大时x的取值范围;
②直接写出直线l与图象L2有四个交点时k的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年,某市某楼盘以每平方米4000元的均价对外销售.因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2015年的均价为每平方米3240元.
(1)求平均每年下调的百分率;
(2)假设2016年的均价仍然下调相同的百分率,李明准备购买一套100平方米的住房,他持有现金10万元,可以在银行贷款20万元,李明的愿望能否实现(房价每平方米按照均价计算)?
查看答案和解析>>
科目:初中数学 来源: 题型:
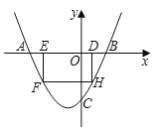
【题目】如图,抛物线![]() 与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
(1)求抛物线的解析式;
(2)当矩形 DEFH 的周长最大时,求矩形 DEFH 的面积;
(3)在(2)的条件下,矩形 DEFH 不动,将抛物线沿着 x 轴向左平移 m 个单位,抛物线与矩形 DEFH的边交于点 M、N,连接 M、N.若 MN 恰好平分矩形 DEFH 的面积,求 m 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要举办一次演讲比赛,每班只能选一人参加比赛.但八年级一班共有甲、乙两人的演讲水平相不相上下,现要在他们两人中选一人去参加全校的演讲比赛,经班主任与全班同学协商决定用摸小球的游戏来确定谁去参赛(胜者参赛).
游戏规则如下:在两个不透明的盒子中,一个盒子里放着两个红球,一个白球;另一个盒子里放着三个白球,一个红球,从两个盒子中各摸一个球,若摸得的两个球都是红球,甲胜;摸得的两个球都是白球,乙胜,否则,视为平局.若为平局,继续上述游戏,直至分出胜负为止.
根据上述规则回答下列问题:
(1)从两个盒子各摸出一个球,一个球为白球,一个球为红球的概率是多少?
(2)该游戏公平吗?请用列表或树状图等方法说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com