
分析 (1)设该农业基地去年种植蔬菜的收入为x万元,种植茶叶的收入为y万元,根据去年种植蔬菜和茶叶的总收入是3400万元结合今年总收入将比去年增加800万元,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设该农业基地去年种植茶叶m亩,每亩的收入为n万元,根据蔬菜与茶叶所需人手之间的关系结合茶叶平均每亩的收入要比蔬菜平均每亩的收入多0.2万元,即可得出该农业基地去年种植蔬菜2.5m亩,每亩的收入为(n-0.2)万元,根据(1)的结论,即可得出关于m、n的二元一次方程组,解之即可得出m值,再求出新增茶叶种植面积及新增的管理茶叶的人数,用其乘2即可得出结论.
解答 解:(1)设该农业基地去年种植蔬菜的收入为x万元,种植茶叶的收入为y万元,
根据题意得:$\left\{\begin{array}{l}{x+y=3400}\\{1.2x+1.3y=3400+800}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2200}\\{y=1200}\end{array}\right.$.
答:该农业基地去年种植蔬菜的收入为2200万元,种植茶叶的收入为1200万元.
(2)设该农业基地去年种植茶叶m亩,每亩的收入为n万元,则该农业基地去年种植蔬菜2.5m亩,每亩的收入为(n-0.2)万元,
根据题意得:$\left\{\begin{array}{l}{mn=1200}\\{2.5m(n-0.2)=2200}\end{array}\right.$,
解得:m=160,
∴0.3m÷10×5×2=48.
答:该农业基地管理蔬菜和茶叶今年共需新增48人.
点评 本题考查了二元一次方程组的应用,解题的关键是:(1)找准数量关系,列出二元一次方程组;(2)根据管理人员之间的比例关系找出去年种植蔬菜的面积是种植茶叶面积的2.5倍.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
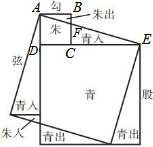 魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理,若图中BF=2,CF=4,则AE的长为6$\sqrt{10}$.
魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理,若图中BF=2,CF=4,则AE的长为6$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com