
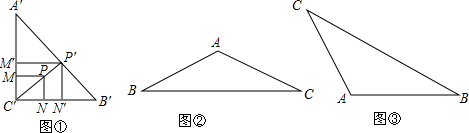
分析 根据已知三角形结合正方形的位置变化分别求出正方形的边长即可.
解答  解:如图②:当四边形EHGF是正方形,则EH=HG=FG=EF=x,
解:如图②:当四边形EHGF是正方形,则EH=HG=FG=EF=x,
∵AB=AC=60,∠A=120°,
∴∠B=∠C=30°,可得BC=60$\sqrt{3}$,
∴BH=CG=$\sqrt{3}$x,
∴x+2$\sqrt{3}$x=60$\sqrt{3}$,
解得:x=$\frac{360-60\sqrt{3}}{11}$≈23.3;
如图③:当四边形GAEF是正方形,则EA=AG=FG=EF=x,
∵AB=AC=60,∠A=120°,
∴∠B=∠C=30°,
∴BE=$\sqrt{3}$x,
∴x+$\sqrt{3}$x=60,
解得:x=30$\sqrt{3}$-30≈21.9,
故方案一中的正方形边长大.
点评 此题主要考查了正方形的性质以及直角三角形的性质,正确表示出三角形的边长是解题关键.


科目:初中数学 来源: 题型:解答题
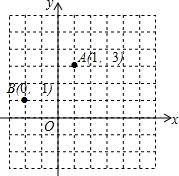 如图,在边长为1的网格中有一个平面直角坐标系.
如图,在边长为1的网格中有一个平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
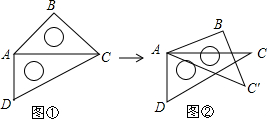
 如图,已知AD平分∠BAC,∠BAC+∠BDC=180°.
如图,已知AD平分∠BAC,∠BAC+∠BDC=180°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com