
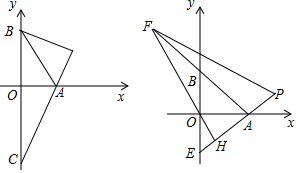
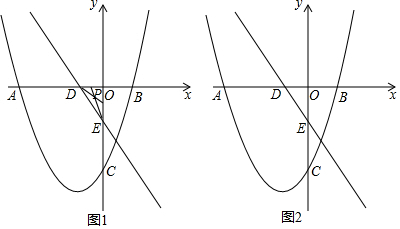
分析 (1)利用非负性得出m,n值,即可得出点A,B坐标,最后用三角形的面积公式即可;
(2)先求出先求出OC,进而得出22.5°的正切值,再求出AC的平方,再求出BD的平方即可;
(3)设出点E坐标,用待定系数法和直线交点坐标即可确定出点P坐标即可得出结论.
解答 解:(1)∵m2-4m+4+$\sqrt{n-2}$=0,
∴(m-2)2+$\sqrt{n-2}$=0,
∴m=n=2,
∴A(2,0),B(0,2),
∴OA=2,OB=2,
∴S△AOB=$\frac{1}{2}$OA×OB=2;
(2)如图1,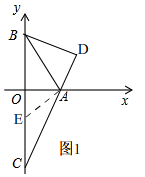 在OC上取一点E,使OE=OA=2,
在OC上取一点E,使OE=OA=2,
由(1)知,OA=OB=2,
∴∠OAB=45°,
∴AE=2$\sqrt{2}$,
∵∠BAD=∠CAO,
∴∠BAD=∠CAO=67.5°,
∵∠ADB=∠AOC=90°,
∴∠ABD=∠ACO=22.5°,
∴CE=AE=2$\sqrt{2}$,
∴OC=OE+CE=2($\sqrt{2}$+1),
∴AC2=OA2+OC2=4+4($\sqrt{2}$+1)2=8(2+$\sqrt{2}$),tan∠ACO=$\frac{OA}{OC}$=$\sqrt{2}$-1,
在Rt△ABD中,tan∠ABD=tan22.5°=tan∠ACO=$\frac{AD}{BD}$=$\sqrt{2}$-1,
∴AD=($\sqrt{2}$-1)BD,
在Rt△AOB中,OA=OB=2,
∴AB=2$\sqrt{2}$,
根据勾股定理得,AD2+BD2=AB2,
∴[($\sqrt{2}$-1)BD]2+BD2=8,
∴BD2=2(2+$\sqrt{2}$),$\frac{B{D}^{2}}{A{C}^{2}}=\frac{2(2+\sqrt{2})}{8(8+\sqrt{2})}$=$\frac{1}{4}$,
∴$\frac{BD}{AC}$=$\frac{1}{2}$;
(3)如图2,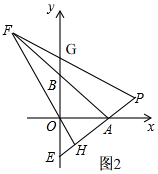 由(1)知,A(2,0),B(0,2),
由(1)知,A(2,0),B(0,2),
∴直线AB解析式为y=-x+2①,
设E(0,a),
∴OE=|a|=-a,
∵BG=OE,
∴BG=-a,
∴OG=2-a,
∴G(0,2-a),
∵A(0,2),E(0,a),
∴直线AE解析式为y=-$\frac{a}{2}$x+a②,
∵OH⊥AE,
∴直线OH解析式为y=$\frac{2}{a}$x③,
联立①③得,x=$\frac{2a}{a+2}$,y=$\frac{4}{a+2}$,
∴F($\frac{2a}{a+2}$,$\frac{4}{a+2}$),
∵G(0,2-a),
∴直线FG的解析式为y=$\frac{a}{2}$x+2-a④,
联立②④得,x=$\frac{2(a-1)}{a}$,y=1,
∴P($\frac{2(a-1)}{a}$,1),
∴点P的纵坐标是定值,定值为1.
点评 此题是三角形综合题,主要考查了非负性的特征,三角形的面积公式,待定系数法,直线交点的确定方法,解本题的关键是用待定系数法确定直线解析式和确定直线的交点坐标,是一道比较简单,但计算量大的常考试题.


科目:初中数学 来源: 题型:选择题
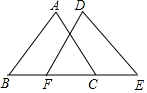 如图,在△ABC和△DEF中,AB=DE,∠B=∠E,补充条件后,能直接应用“SAS”判定△ABC≌△DEF的是( )
如图,在△ABC和△DEF中,AB=DE,∠B=∠E,补充条件后,能直接应用“SAS”判定△ABC≌△DEF的是( )| A. | ∠A=∠D | B. | ∠ACB=∠DEF | C. | AC=DF | D. | BF=EC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
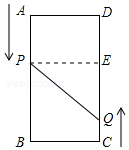 如图,A、B、C、D为矩形的四个顶点,AB=8cm,BC=3cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.
如图,A、B、C、D为矩形的四个顶点,AB=8cm,BC=3cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
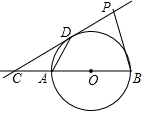 如图,直线CD与线段AB为直径的圆相切于点D,并交BA的延长线于点C,且AB=6,AD=3,P点在切线CD上移动.当∠APB的度数最大时,则∠ABP的度数为( )
如图,直线CD与线段AB为直径的圆相切于点D,并交BA的延长线于点C,且AB=6,AD=3,P点在切线CD上移动.当∠APB的度数最大时,则∠ABP的度数为( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
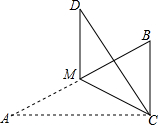 如图,在Rt△ABC中,∠C=90°,∠A<∠B,沿AB边上的中线CM将△ACM翻折,点A落在D处,若BM平分∠CMD,BC=3,则AC的长为( )
如图,在Rt△ABC中,∠C=90°,∠A<∠B,沿AB边上的中线CM将△ACM翻折,点A落在D处,若BM平分∠CMD,BC=3,则AC的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com