
【题目】已知MN∥EF∥BC,点A、D为直线MN上的两动点,AD=a,BC=b,AE∶ED=m∶n;
(1)当点A、D重合,即a=0时(如图1),试求EF.(用含m,n,b的代数式表示)
(2)请直接应用(1)的结论解决下面问题:当A、D不重合,即a≠0,
①如图2这种情况时,试求EF.(用含a,b,m,n的代数式表示)
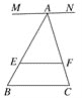
图1
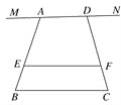
图2
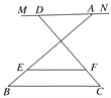
图3
②如图3这种情况时,试猜想EF与a、b之间有何种数量关系?并证明你的猜想.
【答案】(1)EF=![]() ;(2)①EF=
;(2)①EF=![]() ;②猜想:EF=
;②猜想:EF=![]() ,证明详见解析.
,证明详见解析.
【解析】
(1)由EF∥BC,即可证得△AEF∽△ABC,根据相似三角形的对应边成比例,即可证得![]() =
=![]() ,根据比例变形,即可求得EF的值;
,根据比例变形,即可求得EF的值;
(2)①连接BD,与EF交于点H,由(1)知, HF=![]() ,EH=
,EH=![]() ,又由EF=EH+HF,即可求得EF的值;
,又由EF=EH+HF,即可求得EF的值;
②连接DE,并延长DE交BC于G,根据平行线分线段成比例定理,即可求得BG的长,又由EF=![]() 与GC=BC-BG,即可求得EF的值.
与GC=BC-BG,即可求得EF的值.
解 (1)∵EF∥BC,
∴△AEF∽△ABC,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
又BC=b,
∴![]() =
=![]() ,
,
∴EF=![]() ;
;
(2)①如图2,连接BD,与EF交于点H,
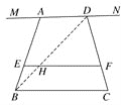
由(1)知,HF=![]() ,EH=
,EH=![]() ,
,
∵EF=EH+HF,
∴EF=![]() ;
;
②猜想:EF=![]() ,
,
证明:连接DE,并延长DE交BC于G,
由已知,得BG=![]() ,
,
EF=![]() ,
,
∵GC=BC-BG,
∴EF=![]() (BC-BG)=
(BC-BG)=![]() =
=![]() .
.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
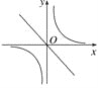
【题目】函数y=kx与y=-![]() 在同一坐标系内的大致图象是( )
在同一坐标系内的大致图象是( )
(1) 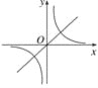 (2)
(2) 
(3) 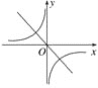 (4)
(4) 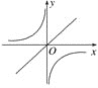
A. (1)和(2)
B. (1)和(3)
C. (2)和(3)
D. (2)和(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当你去看电影的时候,你想坐得离屏幕近一些,可是又不想为了看屏幕边缘的镜头不停地转动眼睛.如图所示,点A、B分别为屏幕边缘两点,若你在P点,则视角为∠APB.如果你觉得电影院内P点是观看的最佳位置,可是已经有人坐在那了,那么你会找到一个位置Q,使得在Q、P两点有相同的视角吗?请在图中画出来(保留画图痕迹,不写画法).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为
的顶点为![]() ,经过原点
,经过原点![]() 且与
且与![]() 轴另一交点为
轴另一交点为![]() .
.
![]() 求点
求点![]() 的坐标;
的坐标;
![]() 若
若![]() 为等腰直角三角形,求抛物线
为等腰直角三角形,求抛物线![]() 的解析式;
的解析式;
![]() 现将抛物线
现将抛物线![]() 绕着点
绕着点![]() 旋转
旋转![]() 后得到抛物线
后得到抛物线![]() ,若抛物线
,若抛物线![]() 的顶点为
的顶点为![]() ,当
,当![]() ,且顶点
,且顶点![]() 在抛物线
在抛物线![]() 上时,求
上时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
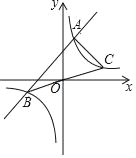
【题目】如图,已知函数y=x+2的图象与函数y=![]() (k≠0)的图象交于A、B两点,连接BO并延长交函数y=
(k≠0)的图象交于A、B两点,连接BO并延长交函数y=![]() (k≠0)的图象于点C,连接AC,若△ABC的面积为8.则k的值为_____.
(k≠0)的图象于点C,连接AC,若△ABC的面积为8.则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
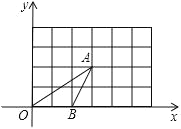
【题目】如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F.
(1)在图中画出△DEF;
(2)点E是否在直线OA上?为什么?
(3)△OAB与△DEF______位似图形(填“是”或“不是”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若AB=4+![]() ,BC=2
,BC=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利客来超市新进一批工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润为4000元?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com