
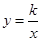
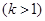 图象上,并与x轴相交于A、B两点. 且始终与y轴相切于定点C(0,1).
图象上,并与x轴相交于A、B两点. 且始终与y轴相切于定点C(0,1).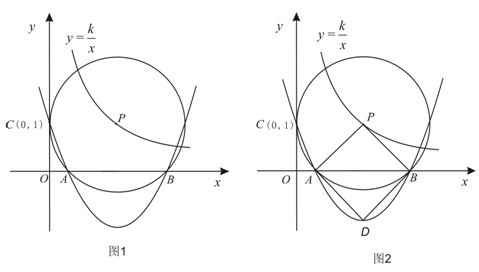
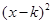 +1-
+1-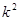 (2)
(2)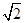
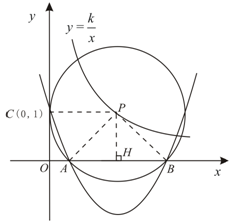
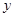 轴相切于点C (0,1),
轴相切于点C (0,1), 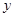 轴.
轴.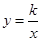 的图象上,
的图象上,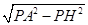 =
= ,
, .
.  ,0). …………………………3分
,0). …………………………3分
 +2
+2 =k+
=k+ ,
, ,0). ……………………………………………………………………4分
,0). ……………………………………………………………………4分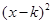 +h. …………………………………………………5分
+h. …………………………………………………5分 ,0), 得:
,0), 得: 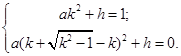
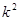 . …………………7分
. …………………7分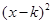 +1-
+1-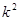 .……8分
.……8分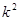 )
)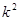 -1.
-1. 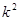 -1=1.
-1=1. 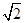 …………………………………………………………11分
…………………………………………………………11分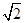 时,PD与AB互相垂直平分,则四边形ADBP为菱形. …………………12分
时,PD与AB互相垂直平分,则四边形ADBP为菱形. …………………12分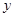 轴,由勾股定理及垂径定理,C (0,1)可得到A
轴,由勾股定理及垂径定理,C (0,1)可得到A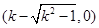 ,B
,B 即可
即可 ,得到关于
,得到关于 的方程即可
的方程即可

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源:不详 题型:解答题
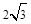 ,0)作圆B的切线交圆于点P,已知tan∠PAB=
,0)作圆B的切线交圆于点P,已知tan∠PAB=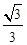 ,抛物线C经过A、P两点。
,抛物线C经过A、P两点。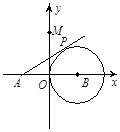
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,
, ),且点B关于原点的对称点C也在该抛物线上.
),且点B关于原点的对称点C也在该抛物线上. 的点共有 个;
的点共有 个;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
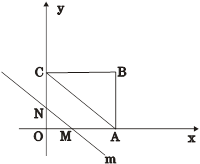
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
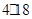 烟花三月经贸旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度
烟花三月经贸旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度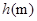 与飞行时间
与飞行时间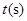 的关系式是
的关系式是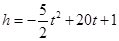 ,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )
,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )A.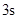 | B.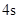 | C.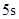 | D.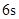 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.1 | B.2 | C.3 | D.4 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com