
【题目】如图,函数y= ![]() (x>0)图象上一点P的横坐标是4,过点P作直线l交x轴于点A,交y轴负半轴于点B,且OA=OB.
(x>0)图象上一点P的横坐标是4,过点P作直线l交x轴于点A,交y轴负半轴于点B,且OA=OB.
(1)求直线l的函数解析式;
(2)过点P作直线l的垂线l1 , 交函数y= ![]() (x>0)图象于点C,求△OPC的面积.
(x>0)图象于点C,求△OPC的面积.
【答案】
(1)解:∵函数y= ![]() (x>0)图象上一点P的横坐标是4,
(x>0)图象上一点P的横坐标是4,
∴点P的坐标为(4,1),
过P作PE⊥y轴于E,

则PE=4,OE=1,
∵OA=OB,∠AOB=90°,
∴∠EBA=∠OAB=45°=∠EPB,
∴PE=EB=4,
∴OB=3,OA=3,
∴B的坐标为(0,﹣3),
设直线l的解析式为y=ax+c,
把B、P的坐标代入得: ![]() ,
,
解得:a=1,c=﹣3,
∴直线l的函数解析式为y=x﹣3;
(2)解:设直线PC交y轴于F,
∵l1⊥l,∠OBA=45°,
∴∠EFP=45°,
∴EF=PE=4,
∴OF=4+1=5,
∴F的坐标为(0,5),
设直线l1的解析式为y=ex+f,
把P和F的坐标代入得: ![]() ,
,
解得:e=﹣1,f=5,
∴直线l1的解析式为y=﹣x+5,
解方程组 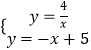 得:
得: ![]() 或
或 ![]() ,
,
即C的坐标为(1,4),
∵F(0,5),C(1,4),P(4,1),B(0,﹣3),
∴△OPC的面积S=S△FPB﹣S△FCO﹣S△POB= ![]() ×(5+3)×4﹣
×(5+3)×4﹣ ![]() ﹣
﹣ ![]() =
= ![]()
【解析】(1)求出P点的坐标,过P作PE⊥y轴于E,求出PE=4,OE=1,PE-EB=4,求出B点的坐标,设直线l的解析式为y=ax+c,把B、P两点的坐标代入即可;(2)设直线PC交y轴于F,求出F点的坐标,求出直线l1的解析式,求出C点的坐标,根据各个点的坐标求出面积即可。
【考点精析】关于本题考查的确定一次函数的表达式,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能得出正确答案.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】从1、2、3、4中任取一个数作为十位上的数字,再从余下的数字中任取一个数作为个位上的数字,那么组成的两位数是6的倍数的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() (x+2)(x﹣4)与x轴交于点A,B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(x+2)(x﹣4)与x轴交于点A,B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(1)求点A,B,C的坐标;
(2)设动点N(﹣2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上一点,请你探究:是否存在点P,使以P,A,B为顶点的三角形与△ABD相似(△PAB与△ABD不重合)?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 的坐标为
的坐标为![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() 为
为![]() 的中点,双曲线
的中点,双曲线![]() 经过
经过![]() 、
、![]() 两点.
两点.

(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)如图1,点![]() 在
在![]() 轴上,若四边形
轴上,若四边形![]() 是平行四边形,求点
是平行四边形,求点![]() 的坐标;
的坐标;
(3)如图2,在(2)的条件下,动点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 在
在![]() 轴上,若以
轴上,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,试求满足要求的所有点
为顶点的四边形为平行四边形,试求满足要求的所有点![]() 、
、![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的结论有_____个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形OABC的顶点B在第一象限,顶点A,C分别在x轴和y轴上,直线l1:x=4与直线l2:y=4相交于点E,以点E为顶点的抛物线K经过点B(6,6).
(1)求抛物线K的解析式.
(2)点P是线段OC上一点,点O关于AP的对称点为M,
①若点M落在直线l1或l2上时,将抛物线向下或向上平移多少,使其顶点落在AM上;
②若点M落在抛物线上,请直接写出一个符合题意的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了解学生对新闻、体育、动画、娱乐、戏曲类电视节目的喜爱情况,采用抽样的方法在七年级选取了一个班的同学,通过问卷调查,收集数据、整理数据,制作了如下两个整统计图,请根据下面两个不完整的统计图分析数据,回答以下问题:

(1)七年级的这个班共有学生_____人,图中![]() ______,
______,![]() ______,在扇形统计图中,“体育”类电视节目对应的圆心角为:______.
______,在扇形统计图中,“体育”类电视节目对应的圆心角为:______.
(2)补全条形统计图;
(3)根据抽样调查的结果,估算该校1750名学生中大约有多少人喜欢“娱乐”类电视节目?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC中,AB=AC,点D,E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.

(1)求证:∠ABE=∠ACD;
(2)求证:过点A、F的直线垂直平分线段BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com