(1)证明:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
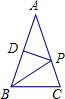
∵AB的垂直平分线DP交AC于点P,
∴PA=PB,
∴∠PBA=∠A=36°,
∴∠PBC=∠ABC-∠PBA=72°-36°=36°,
∴∠PBC=∠A,
∵∠C=∠C,
∴△ABC∽△BPC;
(2)解:∵m,n为一元二次方程x
2+x-1=0的两根(m>n),
解方程可得:m=

,n=
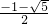
.
∵△ABC∽△BPC,
∴
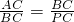
,PB=BC,
设PC=x,则AC=AP+PC=BP+PC=BC+PC=BC+x,
∴
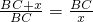
,
∴BC=

x,
∴AC=
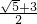
x,
∴

=

=m.
∴△BPC是“黄金三角形”.
分析:(1)由在△ABC中,AB=AC,∠A=36°,即可求得∠ABC的度数,又由AB的垂直平分线DP交AC于点P,求得∠ABP的度数,即可得∠PBC=∠A=36°,即可证得:△ABC∽△BPC与△PBC是等腰三角形;
(2)由m,n为一元二次方程x
2+x-1=0的两根(m>n),即可求得m的值,又由△ABC∽△BPC,根据相似三角形的对应边成比例,设PC=x,然后求得BC与AC的长,求比值即可证得△BPC是“黄金三角形”.
点评:此题考查了相似三角形的判定与性质,等腰三角形的判定与性质,线段垂直平分线的定义以及二次函数的解法等知识.此题综合性很强,难度适中,解题的关键是方程思想与数形结合思想的应用.

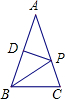 如图,在△ABC中,AB=AC,∠A=36°.AB的垂直平分线DP交AC于点P,
如图,在△ABC中,AB=AC,∠A=36°.AB的垂直平分线DP交AC于点P,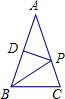
 ,n=
,n=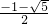 .
.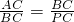 ,PB=BC,
,PB=BC,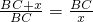 ,
, x,
x,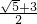 x,
x, =
= =m.
=m.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为