练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．下列等式成立的是（　　）
    A．6÷（-$\frac{1}{4}$）×4=6×（-4）×4B．6÷（-$\frac{1}{4}$）×4=6×（-$\frac{1}{4}$）×4C．6÷（-$\frac{1}{4}$）×4=6÷（-$\frac{1}{4}$×4）D．6÷（-$\frac{1}{4}$）×4=6×（-4）÷4

    分析 根据有理数的除法法则，可得答案．

    解答 解：6÷（-$\frac{1}{4}$）×4=6×（-4）×4，
    故选：A．

    点评 本题考查了有理数的除法，解题关键是把除法转化成乘法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017届江苏省无锡市九年级下学期第一次模拟考试数学试卷（解析版） 题型：解答题

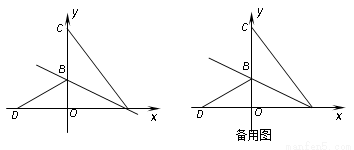
    如图，在平面直角坐标系中，O为坐标原点，△ABC的边BC在y轴的正半轴上，点A在x轴的正半轴上，点C的坐标为（0，8），将△ABC沿直线AB折叠，点C落在x轴的负半轴D（?4，0）处．

    （1）求直线AB的解析式；

    （2）点P从点A出发以每秒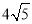个单位长度的速度沿射线AB方向运动，过点P作PQ⊥AB，交x轴于点Q，PR∥AC交x轴于点R，设点P运动时间为t（秒），线段QR长为d，求d与t的函数关系式（不要求写出自变量t的取值范围）；

    （3）在（2）的条件下，点N是射线AB上一点，以点N为圆心，同时经过R、Q两点作⊙N，⊙N交y轴于点E，F．是否存在t，使得EF=RQ？若存在，求出t的值，并求出圆心N的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年北京市西城区七年级上学期期末考试数学试卷（解析版） 题型：填空题

    下面的框图表示解方程3x-7（x-1）=3-2（x+3）的流程，其中A代表的步骤是_________，步骤A对方程进行变形的依据是________________。

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，边长都为1的正方形AEFG与正方形ABCD，正方形AEFG绕顶点A旋转一周，在此旋转过程中，线段DF的长可取的整数值为1和2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．一次越野赛跑中，当小明跑了1600m时，小刚跑了1450m．此后两人分别以am/s和bm/s匀速跑．又过100s时小刚追上小明，200s时小刚到达终点，300s时小明到达终点．求这次越野赛跑的全程．
    （Ⅰ）根据题意，填写下表：
    时间（秒）
    路程（米）    		从比赛开始到
    匀速跑前    		从比赛开始到
    匀速跑完100秒    		从比赛开始到
    匀速跑完200秒
    小明16001600+100a1600+200a
    小刚14501450+100b1450+200b
    （Ⅱ）求出问题的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

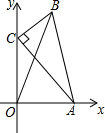    5．如图，在△ABC中，∠C=90°，AC=4，BC=2，点A、C分别在x轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动，在运动过程中，点B到原点的最大距离是（　　）
    A．2$\sqrt{2}$+2B．2$\sqrt{5}$C．2$\sqrt{6}$D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，圆O的半径为2$\sqrt{2}$，AB、AC是圆O的两条弦，AB=2$\sqrt{3}$，AC=4，如果以O为圆心，作一个与AC相切的圆，那么这个圆的半径是多少？它与AB又怎样的位置关系？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

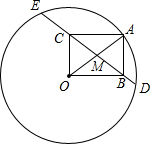    8．如图，⊙O的半径为10，A是⊙O上一点．以OA为对角线作矩形OBAC，且OC=6．延长BC，与⊙O分别交于D，E两点，则△OCE和△OBD的周长差等于（　　）
    A．$\frac{3}{5}$B．$\frac{4}{5}$C．1D．$\frac{6}{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．观察下列计算，去掉分母中的根号．
    $\frac{1}{\sqrt{2}+\sqrt{1}}$=$\frac{\sqrt{2}-1}{（\sqrt{2}+1）（\sqrt{2}-1）}$=$\sqrt{2}$-1，$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}-\sqrt{2}}{（\sqrt{3}+\sqrt{2}）（\sqrt{3}-\sqrt{2}）}$=$\sqrt{3}$-$\sqrt{2}$，
    $\frac{1}{\sqrt{4}+\sqrt{3}}$=$\frac{\sqrt{4}-\sqrt{3}}{（\sqrt{4}+\sqrt{3}）（\sqrt{4}-\sqrt{3}）}$=$\sqrt{4}$-$\sqrt{3}$=2-$\sqrt{3}$
    （1）第n个式子：$\frac{1}{\sqrt{n+1}+\sqrt{n}}$（n≥2的自然数）应写成什么形式？
    （2）从上述结果中找出规律，并利用这一规律计算：
    （$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$）+…+$\frac{1}{\sqrt{2009}+\sqrt{2008}}$）•（$\sqrt{2009}$+1）
    （3）通过（1）（2）问题的解答，你能否找到计算式子：
    $\frac{1}{2\sqrt{1}+1\sqrt{2}}$+$\frac{1}{3\sqrt{2}+2\sqrt{3}}$+$\frac{1}{4\sqrt{3}+3\sqrt{4}}$+…+$\frac{1}{2009\sqrt{2008}+2008\sqrt{2009}}$．

    查看答案和解析>>

    同步练习册答案