
分析 (1)首先化简二次根式,计算0次幂,代入特殊角的三角函数,然后合并同类二次根式即可;
(2)首先把第一个分式的分母、分母分解因式,括号内的式子通分相加,然后除法转化为乘法,计算乘法即可化简,最后代入数值计算即可.
解答 解:(1)原式=$\sqrt{2}$+1+2×$\frac{\sqrt{2}}{2}$+4=$\sqrt{2}$+1+$\sqrt{2}$+4=2$\sqrt{2}$+5;
(2)原式=$\frac{(x-y)^{2}}{x-y}$÷$\frac{(x+y)(x-y)}{xy}$
=(x-y)•$\frac{xy}{(x+y)(x-y)}$
=$\frac{xy}{x+y}$.
当x=$\sqrt{2}$+1,y=$\sqrt{2}$-1时,原式=$\frac{(\sqrt{2}+1)(\sqrt{2}-1)}{2\sqrt{2}}$=$\frac{\sqrt{2}}{4}$.
点评 本题考查了二次根式的化简求值以及分式的化简求值,正确对分式的分子、分母分解因式是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
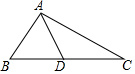 如图所示,在△ABC中,∠B=47°,∠C=23°,AD是△ABC的角平分线,则∠CAD的度数为( )
如图所示,在△ABC中,∠B=47°,∠C=23°,AD是△ABC的角平分线,则∠CAD的度数为( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{360}{n}$=$\frac{12}{5}$ | B. | $\frac{35}{{S}_{面}}$=$\frac{5}{12}$ | C. | $\frac{5}{12}$=$\frac{n}{180}$ | D. | S面=35$÷\frac{5}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查某种计算机的使用寿命 | B. | 调查CCTV某档电视节目的收视情况 | ||
| C. | 调查我国七年级学生的视力情况 | D. | 调查你所在的班级学生的视力情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com