
| 2 |
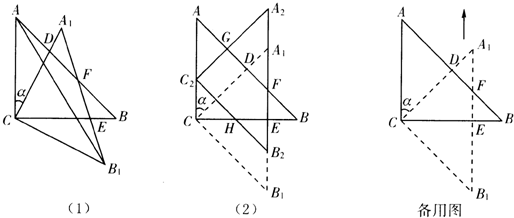
| 1 |
| 2 |
| 180°-∠ACB1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AC2+BC2 |
| 2 |
| 1 |
| 2 |
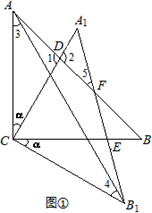
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
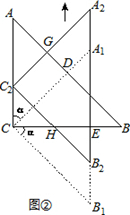
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |


科目:初中数学 来源:浙江省中考真题 题型:解答题


查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,如图1,将![]() 个边长为1的正方形并排组成矩形OABC, 相邻两边OA和OC分别落在
个边长为1的正方形并排组成矩形OABC, 相邻两边OA和OC分别落在![]() 轴和
轴和![]() 轴的正半轴上, 设抛物线
轴的正半轴上, 设抛物线![]() (
(![]() <0)过矩形顶点B、C.
<0)过矩形顶点B、C.
(1)当n=1时,如果![]() =-1,试求b的值;
=-1,试求b的值;
(2)当n=2时,如图2,在矩形OABC上方作一边长为1的正方形EFMN,使EF在线段CB上,如果M,N两点也在抛物线上,求出此时抛物线的解析式;
(3)将矩形OABC绕点O顺时针旋转,使得点B落到![]() 轴的正半轴上,如果该抛物线同时经过原点O.①试求当n=3时a的值;
轴的正半轴上,如果该抛物线同时经过原点O.①试求当n=3时a的值;
②直接写出![]() 关于
关于![]() 的关系式.
的关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
 个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在
个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在 轴和
轴和 轴的正半轴上, 设抛物
轴的正半轴上, 设抛物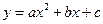
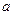 <0)过矩形顶点B、C.
<0)过矩形顶点B、C.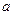 =-1,试求b的值;
=-1,试求b的值; 轴的正半轴上,如果该抛物线同时经过原点O.①试求当n=3时a的值;
轴的正半轴上,如果该抛物线同时经过原点O.①试求当n=3时a的值;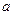 关于
关于 的关系式.
的关系式.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(浙江金华卷)数学 题型:解答题
(本题10分)在平面直角坐标系中,如图1,将 个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在
个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在 轴和
轴和 轴的正半轴上, 设抛物
轴的正半轴上, 设抛物
( <0)过矩形顶点B、C.
<0)过矩形顶点B、C.
(1)当n=1时,如果 =-1,试求b的值;
=-1,试求b的值;
(2)当n=2时,如图2,在矩形OABC上方作一边长为1的正方形EFMN,使EF在线段CB上,如果M,N两点也在抛物线上,求出此时抛物线的解析式;
(3)将矩形OABC绕点O顺时针旋转,使得点B落到 轴的正半轴上,如果该抛物线同时经过原点O.①试求当n=3时a的值;
轴的正半轴上,如果该抛物线同时经过原点O.①试求当n=3时a的值;
②直接写出 关于
关于 的关系式.
的关系式.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(浙江舟山卷)数学解析版 题型:解答题
(本题10分)在平面直角坐标系中,如图1,将 个边长为1的正方形并排组成矩形OABC, 相邻两边OA和OC分别落在
个边长为1的正方形并排组成矩形OABC, 相邻两边OA和OC分别落在 轴和
轴和 轴的正半轴上, 设抛物
轴的正半轴上, 设抛物
( <0)过矩形顶点B、C.
<0)过矩形顶点B、C.
(1)当n=1时,如果 =-1,试求b的值;
=-1,试求b的值;
(2)当n=2时,如图2,在矩形OABC上方作一边长为1的正方形EFMN,使EF在线段CB上,如果M,N两点也在抛物线上,求出此时抛物线的解析式;
(3)将矩形OABC绕点O顺时针旋转,使得点B落到 轴的正半轴上,如果该抛物线同时经过原点O.①试求当n=3时a的值;
轴的正半轴上,如果该抛物线同时经过原点O.①试求当n=3时a的值;
②直接写出 关于
关于 的关系式.
的关系式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com