
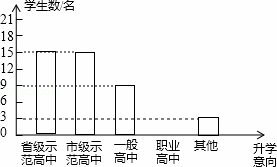
近几年我市加大中职教育投入力度,取得了良好的社会效果.某校随机调查了九年级m名学生的升学意向,并根据调查结果绘制出如下不完整的统计图表:
升学意向 人数 百分比
省级示范高中 15 25%
市级示范高中 15 25%
一般高中 9 n
职业高中
其他 3 5%
m 100%
请你根据图表中提供的信息解答下列问题:
(1)表中m的值为 ,n的值为 ;
(2)补全条形统计图;
(3)若该校九年级有学生500名,估计该校大约有多少名毕业生的升学意向是职业高中?


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
图1和图2中,优弧 所在⊙O的半径为2,AB=2
所在⊙O的半径为2,AB=2 .点P为优弧
.点P为优弧 上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.
上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.
(1)点O到弦AB的距离是 1 ,当BP经过点O时,∠ABA′= 60 °;
(2)当BA′与⊙O相切时,如图2,求折痕的长:
(3)若线段BA′与优弧 只有一个公共点B,设∠ABP=α.确定α的取值范围.
只有一个公共点B,设∠ABP=α.确定α的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面的半径是 .



查看答案和解析>>
科目:初中数学 来源: 题型:
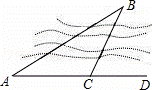
如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( )
A. 100米 B. 50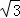 米 C.
米 C. 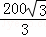 米 D. 50米
米 D. 50米


查看答案和解析>>
科目:初中数学 来源: 题型:
某小区2010年屋顶绿化面积为2000平方米,计划2012年屋顶绿化面积要达到2880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是 .


查看答案和解析>>
科目:初中数学 来源: 题型:
已知两条平行线l1、l2之间的距离为6,截线CD分别交l1、l2于C、D两点,一直角的顶点P在线段CD上运动(点P不与点C、D重合),直角的两边分别交l1、l2与A、B两点.
(1)操作发现
如图1,过点P作直线l3∥l1,作PE⊥l1,点E是垂足,过点B作BF⊥l3,点F是垂足.此时,小明认为△PEA∽△PFB,你同意吗?为什么?
(2)猜想论证
将直角∠APB从图1的位置开始,绕点P顺时针旋转,在这一过程中,试观察、猜想:当AE满足什么条件时,以点P、A、B为顶点的三角形是等腰三角形?在图2中画出图形,证明你的猜想.
(3)延伸探究
在(2)的条件下,当截线CD与直线l1所夹的钝角为150°时,设CP=x,试探究:是否存在实数x,使△PAB的边AB的长为4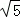 ?请说明理由.
?请说明理由.
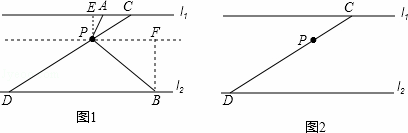


查看答案和解析>>
科目:初中数学 来源: 题型:
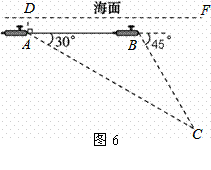
如图6,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据: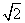 ≈1.414,
≈1.414, ≈1.732,
≈1.732,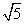 ≈2.236).
≈2.236).
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com