
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:阅读理解

 H2(g)+CO2(g),该反应的化学平衡常数表达式为K= ;反应的平衡常数随温度的变化如表一,
H2(g)+CO2(g),该反应的化学平衡常数表达式为K= ;反应的平衡常数随温度的变化如表一,| 温度/℃ | 400 | 500 | 830 | 1000 |
| 平衡常数K | 10 | 9 | 1 | 0.6 |
 H2(g)+CO2(g),在830℃,以表二的物质的量(单位为mol)投入恒容反应器发生上述反应,其中反应开始时,向正反应方向进行的有 (填实验编号);
H2(g)+CO2(g),在830℃,以表二的物质的量(单位为mol)投入恒容反应器发生上述反应,其中反应开始时,向正反应方向进行的有 (填实验编号);| 实验编号 | N(CO) | N(H2O) | n(H2) | N(CO2) |
| A | 1 | 5 | 2 | 3 |
| B | 2 | 2 | 1 | 1 |
| C | 0.5 | 2 | 1 | 1 |
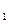 达到平衡、在时刻t
达到平衡、在时刻t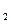 分别因改变某个条件而发生变化的情况:图中时刻t
分别因改变某个条件而发生变化的情况:图中时刻t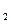 发生改变的条件是_________。(写出两种)
发生改变的条件是_________。(写出两种)
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
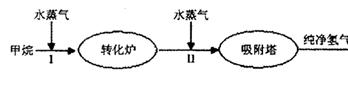
 H2(g)+CO2(g),该反应的化学平衡常数表达式为K= ;反应的平衡常数随温度的变化如表一,
H2(g)+CO2(g),该反应的化学平衡常数表达式为K= ;反应的平衡常数随温度的变化如表一,| 温度/℃ | 400 | 500 | 830 | 1000 |
| 平衡常数K | 10 | 9 | 1 | 0.6 |
 H2(g)+CO2(g),在830℃,以表二的物质的量(单位为mol)投入恒容反应器发生上述反应,其中反应开始时,向正反应方向进行的有 (填实验编号);
H2(g)+CO2(g),在830℃,以表二的物质的量(单位为mol)投入恒容反应器发生上述反应,其中反应开始时,向正反应方向进行的有 (填实验编号);| 实验编号 | N(CO) | N(H2O) | n(H2) | N(CO2) |
| A | 1 | 5 | 2 | 3 |
| B | 2 | 2 | 1 | 1 |
| C | 0.5 | 2 | 1 | 1 |
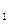 达到平衡、在时刻t
达到平衡、在时刻t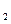 分别因改变某个条件而发生变化的情况:图中时刻t
分别因改变某个条件而发生变化的情况:图中时刻t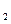 发生改变的条件是_________。(写出两种)
发生改变的条件是_________。(写出两种)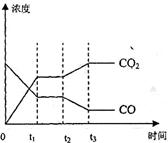
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:北京同步题 题型:填空题
 =( )
=( )  ( )
( ) ( )
( )  ( )
( )


查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
【考点】菱形的性质;全等三角形的判定与性质;等边三角形的判定与性质.
【分析】根据菱形的四条边都相等,先判定△ABD是等边三角形,再根据菱形的性质可得∠BDF=∠C=60°,再求出DF=CE,然后利用“边角边”即可证明△BDF≌△DCE,从而判定①正确;根据全等三角形对应角相等可得∠DBF=∠EDC,然后利用三角形的一个外角等于与它不相邻的两个内角的和可以求出∠DMF=∠BDC=60°,再根据平角等于180°即可求出∠BMD=120°,从而判定②正确;根据三角形的一个外角等于与它不相邻的两个内角的和以及平行线的性质求出∠ABM=∠ADH,再利用“边角边”证明△ABM和△ADH全等,根据全等三角形对应边相等可得AH=AM,对应角相等可得∠BAM=∠DAH,然后求出∠MAH=∠BAD=60°,从而判定出△AMH是等边三角形,判定出③正确;根据全等三角形的面积相等可得△AMH的面积等于四边形ABMD的面积,然后判定出④错误.
【解答】在菱形ABCD中,∵AB=BD,
∴AB=BD=AD,
∴△ABD是等边三角形,
∴根据菱形的性质可得∠BDF=∠C=60°,
∵BE=CF,
∴BC-BE=CD-CF,
即CE=DF,
在△BDF和△DCE中,CE=DF;∠BDF=∠C=60°;BD=CD,
∴△BDF≌△DCE(SAS),故①小题正确;
∴∠DBF=∠EDC,
∵∠DMF=∠DBF+∠BDE=∠EDC+∠BDE=∠BDC=60°,
∴∠BMD=180°-∠DMF=180°-60°=120°,故②小题正确;
∵∠DEB=∠EDC+∠C=∠EDC+60°,∠ABM=∠ABD+∠DBF=∠DBF+60°,
∴∠DEB=∠ABM,
又∵AD∥BC,
∴∠ADH=∠DEB,
∴∠ADH=∠ABM,
在△ABM和△ADH中,AB=AD;∠ADH=∠ABM;DH=BM,
∴△ABM≌△ADH(SAS),
∴AH=AM,∠BAM=∠DAH,
∴∠MAH=∠MAD+∠DAH=∠MAD+∠BAM=∠BAD=60°,
∴△AMH是等边三角形,故③小题正确;
∵△ABM≌△ADH,
∴△AMH的面积等于四边形ABMD的面积,
又∵△AMH的面积=![]() AM·
AM·![]() AM=
AM=![]() AM2,
AM2,
∴S四边形ABMD=![]() AM2,S四边形ABCD≠S四边形ABMD,故④小题错误,
AM2,S四边形ABCD≠S四边形ABMD,故④小题错误,
综上所述,正确的是①②③共3个.
故选C.
【点评】本题考查了菱形的性质,全等三角形的判定与性质,等边三角形的判定与性质,题目较为复杂,特别是图形的识别有难度,从图形中准确确定出全等三角形并找出全等的条件是解题的关键.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com