
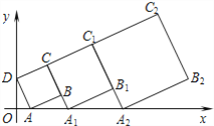
【题目】在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,………按这样的规律进行下去,正方形A2018B2018C2018C2017的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】试题分析:∵点A的坐标为(1,0),点D的坐标为(0,2),
∴OA=1,OD=2,
设正方形的面积分别为S1,S2…S2019,
在直角△ADO中,根据勾股定理,
得:AD=![]() =
=![]() ,
,
∴AB=AD=BC=![]() ,
,
∴正方形ABCD的面积为:S1=5;
∵∠DAO+∠ADO=90°,∠DAO+∠BAA1=90°,
∴∠ADO=∠BAA1,
∵∠AOD=∠ABA1=90°,
∴△AOD∽△ABA1,
∴![]() ,
,
即![]() ,
,
∴BA1=![]() ,
,
∴A1C=BC+ BA1=![]() ,
,
∴正方形A1B1C1C的面积为:S2=![]() ×5=5×
×5=5×![]() ,
,
根据题意,得:AD∥BC∥C1A2∥C2B2,
∴∠BAA1=∠B1A1A2=∠B2A2x,
∵∠ABA1=∠A1B1A2=90°,
∴△BAA1∽△B1A1A2,
∴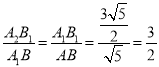 ,
,
∴A2B1=![]() =
=![]() ,
,
∴A2C1=B1C1+A2B1=![]() +
+![]() =
=![]() ,
,
∴正方形A2B2C2C1的面积为:S3=![]() ×5=5×
×5=5×![]() ,
,
由此可得:Sn=5×![]() ,
,
∴正方形A2018B2018C2018C2017的面积为S2019=5×![]() =5×
=5×![]() .
.
故选C.


科目:初中数学 来源: 题型:
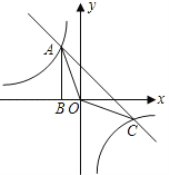
【题目】如图,Rt△ABO的顶点A是双曲线y1=![]() 与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求△AOC的面积.
(3)直接写出使y1>y2成立的x的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 和三角形
和三角形![]() 在同一平面内.
在同一平面内.

(1)如图1,点![]() 在
在![]() 边上,
边上,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() .若
.若![]() ,求
,求![]() 的度数.
的度数.
(2)如图2,点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,
,![]() ,证明:
,证明:![]() .
.
(3)点![]() 是三角形
是三角形![]() 外部的任意一点,过
外部的任意一点,过![]() 作
作![]() 交直线
交直线![]() 于
于![]() ,
,![]() 交直线
交直线![]() 于
于![]() ,直接写出
,直接写出![]() 与
与![]() 的数量关系(不需证明).
的数量关系(不需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中,有两个完全相同的直角三角形纸片,如果把其中一个三角形纸片先横向平移![]() 格,再纵向平移
格,再纵向平移![]() 格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么
格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么![]() 的结果( )
的结果( )

A.只有一个确定的值B.有两个不同的值
C.有三个不同的值D.有三个以上不同的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组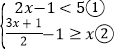
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在数轴上表示的数是﹣6,点B表示的数是+10,P,Q两点同时分别以1个单位/秒和2个单位/秒的速度从A,B两点出发,沿数轴做匀速运动,设运动时间为t(秒).
(1)线段AB的长度为 个单位;
(2)如果点P向右运动,点Q向左运动,求:
①当t为何值时,P与点Q相遇?
②当t为何值时,PQ=![]() AB?
AB?
(3)如果点P,点Q同时向左运动,是否存在这样的时间t使得P,Q两点到A点距离相等?若存在,求出t的值,若不存在,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有一![]() ,且
,且![]() ,
,![]() ,
,![]() ,已知
,已知![]() 是由
是由![]() 绕某点顺时针旋转得到的.
绕某点顺时针旋转得到的.

(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)以(1)中的旋转中心为中心,分别画出![]() 顺时针旋转90°、180°的三角形;
顺时针旋转90°、180°的三角形;
(3)设![]() 两直角边
两直角边![]() 、
、![]() 、斜边
、斜边![]() ,利用变换前后所形成的图案验证勾股定理.
,利用变换前后所形成的图案验证勾股定理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华同学经过调查,了解到某客车租赁公司有![]() ,
,![]() 两种型号的客车,并得到了下表中的信息.
两种型号的客车,并得到了下表中的信息.
车型 |
|
|
|
| |
座位 | 45座 | 60座 |
信息 | 每辆 | |
5辆 | ||
(1)求每辆![]() 型和
型和![]() 型客车每天的租金各是多少元?
型客车每天的租金各是多少元?
(2)小华所在学校准备组织七年级全体学生外出一天进行研学活动,小华同学设计了下面甲乙两种租车方案:
方案甲:只租用![]() 型客车,但有一辆客车会空出30个座位.
型客车,但有一辆客车会空出30个座位.
方案乙:只租用![]() 型客车,刚好坐满,且比方案甲少用两辆客车.
型客车,刚好坐满,且比方案甲少用两辆客车.
求小华所在学校七年级学生的总人数.
(3)如果从节省费用的角度考虑,是否还有其他租车方案?如果有,请直接写出一种租车方案;如果没有,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com