【题目】如图，在
中，点
是
的中点，
且交
于点
，求证：
是的中位线．
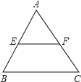
【答案】证明见解析.
【解析】
过点B作BG∥CF交FE的延长线于G，判断出四边形BCFG是平行四边形，根据平行四边形的对边相等可得BG=CF，根据两直线平行，内错角相等可得∠A=∠EBG，再利用“边角边”证明△AEF和△BEG全等，根据全等三角形对应边相等可得BG=AF，从而得到AF=CF，再根据三角形的中位线的定义证明．
如图，过点B作BG∥CF交FE的延长线于G．
∵EF∥BC，∴四边形BCFG是平行四边形，∴BG=CF，∴BG∥CF，∴∠A=∠EBG．
∵点E是AB的中点，∴AE=BE．
在△AEF和△BEG中，∵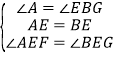
，∴△AEF≌△BEG（ASA），∴BG=AF，∴AF=CF．
又∵点E是AB的中点，∴EF是△ABC的中位线．
科目：初中数学 来源： 题型：
【题目】如图（1），一架云梯AB斜靠在一竖直的墙上，云梯的顶端A距地面15米，梯子的长度比梯子底端B离墙的距离大5米.
（1）这个云梯的底端B离墙多远?
（2）如图（2），如果梯子的顶端下滑了8m（AC的长），那么梯子的底部在水平方向右滑动了多少米?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，点
是线段
的中点，
，
.
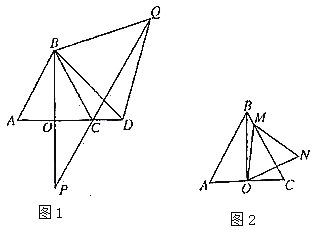
（1）如图1，若
，求证
是等边三角形；
（2）如图1，在（1）的条件下，若点
在射线上，点在点
右侧，且
是等边三角形，
的延长线交直线
于点
，求
的长度；
（3）如图2，在（1）的条件下，若点
在线段
上，
是等边三角形，且点沿着线段从点
运动到点，点
随之运动，求点的运动路径的长度.
查看答案和解析>>
科目：初中数学 来源： 题型：
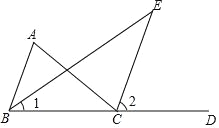
【题目】如图，已知在△ABC中，CE是外角∠ACD的平分线，BE是∠ABC的平分线．
(1)求证：∠A＝2∠E，以下是小明的证明过程，请在括号里填写理由．
证明：∵∠ACD是△ABC的一个外角，∠2是△BCE的一个外角，(已知)
∴∠ACD＝∠ABC+∠A，∠2＝∠1+∠E(_________)
∴∠A＝∠ACD﹣∠ABC，∠E＝∠2﹣∠1(等式的性质)
∵CE是外角∠ACD的平分线，BE是∠ABC的平分线(已知)
∴∠ACD＝2∠2，∠ABC＝2∠1(_______)
∴∠A＝2∠2﹣2∠1(_________)
＝2(∠2﹣∠1)(_________)
＝2∠E(等量代换)
(2)如果∠A＝∠ABC，求证：CE∥AB．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店购进
，
两种商品，购买
个商品比购买个商品多花
元，并且花费
元购买商品和花费
元购买商品的数量相等.
（1）求购买一个商品和一个商品各需要多少元？
（2）若商店准备购买，两种商品共
个，并且购买，两种商品的总费用不超过
元，那么商店至多购买商品多少件？
查看答案和解析>>
科目：初中数学 来源： 题型：
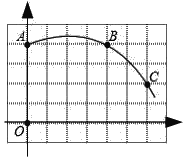
【题目】如图，网格纸中每个小正方形的边长为1，一段圆弧经过格点，点O为坐标原点．
（1）该图中弧所在圆的圆心D的坐标为 ；．
（2）根据（1）中的条件填空：
①圆D的半径= （结果保留根号）；
②点（7，0）在圆D （填“上”、“内”或“外”）；
③∠ADC的度数为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
