
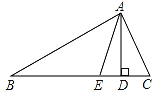
【题目】已知:如图,在△ABC中,AD、AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,求∠DAE的度数.
(2)试问∠DAE与∠C﹣∠B有怎样的数量关系?说明理由.
【答案】(1)10°;(2)∠DAE=![]() (∠C-∠B).
(∠C-∠B).
【解析】试题分析:(1)先根据三角形内角和得到∠CAB=180°﹣∠B﹣∠C=100°,再根据角平分线与高线的定义得到∠CAE=![]() ∠CAB=50°,∠ADC=90°,则∠CAD=90°﹣∠C=40°,然后利用∠DAE=∠CAE﹣∠CAD计算即可.
∠CAB=50°,∠ADC=90°,则∠CAD=90°﹣∠C=40°,然后利用∠DAE=∠CAE﹣∠CAD计算即可.
(2)根据题意可以用∠B和∠C表示出∠CAD和∠CAE,从而可以得到∠DAE与∠C﹣∠B的关系.
试题解析:解:∵∠ABC=30°,∠ACB=50°,∴∠CAB=180°﹣∠B﹣∠C=100°,∵AE是△ABC角平分线,∴∠CAE=![]() ∠CAB=50°,∵AD是△ABC的高,∴∠ADC=90°,∴∠CAD=90°﹣∠C=40°,∴∠DAE=∠CAE﹣∠CAD=50°﹣40°=10°.
∠CAB=50°,∵AD是△ABC的高,∴∠ADC=90°,∴∠CAD=90°﹣∠C=40°,∴∠DAE=∠CAE﹣∠CAD=50°﹣40°=10°.
(2)∠DAE=![]() (∠ACB﹣∠ABC),理由:∵在△ABC中,AD,AE分别是△ABC的高和角平分线,∴∠CAB=180°﹣∠B﹣∠C,∠CAD=90°﹣∠C,∠CAE=
(∠ACB﹣∠ABC),理由:∵在△ABC中,AD,AE分别是△ABC的高和角平分线,∴∠CAB=180°﹣∠B﹣∠C,∠CAD=90°﹣∠C,∠CAE=![]() (180°﹣∠B﹣∠C),∴∠DAE=
(180°﹣∠B﹣∠C),∴∠DAE=![]() (180°﹣∠B﹣∠C)﹣(90°﹣∠C)=
(180°﹣∠B﹣∠C)﹣(90°﹣∠C)=![]() (∠C﹣∠B).
(∠C﹣∠B).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】不相等的有理数a,b,c在数轴上的对应点分别是A、B、C,如果|a﹣b|+|b﹣c|=|a﹣c|,那么点B ( )
A.在A、C点的左边
B.在A、C点的右边
C.在A、C点之间
D.上述三种均可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①a为任意有理数,a2+1总是正数;②如果a+|a|=0,则a<0;③两点确定一条直线;④若MA=MB,则点M是线段AB的中点.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面.
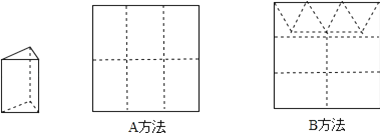
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)设裁剪出的侧面个数为![]() 个,裁剪出底面的个数为
个,裁剪出底面的个数为![]() 个.分别求出
个.分别求出![]() 、
、![]() 与x的关系式.
与x的关系式.
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有三个球,其中2个红球,1个白球,它们除颜色不同外其余都相同:
(1)摸出一个球记下颜色后放回,并搅匀,再摸出一个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(2)现再将n个白球放入布袋中搅匀后使摸出一个球是白球的概率为![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
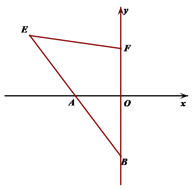
【题目】已知,如图A在x轴负半轴上,B(0,-4),点E(-6,4)在射线BA上,
(1) 求证:点A为BE的中点
(2) 在y轴正半轴上有一点F, 使 ∠FEA=45°,求点F的坐标.
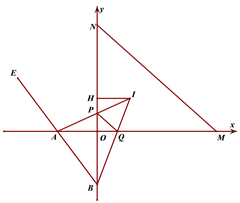
(3) 如图,点M、N分别在x轴正半轴、y轴正半轴上,MN=NB=MA,点I为△MON的内角平分线的交点,AI、BI分别交y轴正半轴、x轴正半轴于P、Q两点, IH⊥ON于H, 记△POQ的周长为C△POQ.求证:C△POQ=2 HI.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com