练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

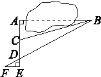
    【题目】数学课外兴趣小组的同学们要测量被池塘隔开的两棵树A，B之间的距离，他们设计了如图所示的测量方案：从树A沿着垂直于AB的方向走到点E处，再从点E沿着垂直于AE的方向走到点F处，C为AE上一点，其中三位同学分别测得三组数据：①AC，∠ACB；②EF，DE，AD；③CD，∠ACB，∠ADB.其中能根据所测数据求得A，B两树之间的距离的有________组．

    【答案】3

    【解析】（1）可利用∠ACB的正切来求AB的长；（2）可利用∠ACB和∠ADB的正切求出AB；（3）设AC=x，AD=CD+x，AB=，AB=.

    此题比较综合，要多方面考虑，
    第①组中，因为知道∠ACB和AC的长，所以可利用∠ACB的正切来求AB的长；
    第②组中可利用∠ACB和∠ADB的正切求出AB；
    第③组中设AC=x，AD=CD+x，AB=，AB=；

    因为已知CD，∠ACB，∠ADB，可求出x，然后得出AB．

    故答案为：3

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】问题情境:以直线AB上一点O为端点作射线OM、ON，将一个直角三角形的直角顶点放在O处(∠COD=90°).

    (1)如图1，直角三角板COD的边OD放在射线OB上，OM平分∠AOC，ON和OB重合，则∠MON=_°；

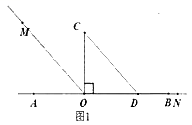
    (2)直角三角板COD绕点O旋转到如图2的位置，OM平分∠AOC，ON平分∠BOD，求∠MON的度数。

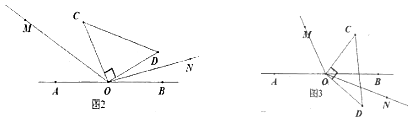
    (3)直角三角板COD绕点O旋转到如图3的位置，OM平分∠ AOC ，ON平分∠BOD，猜想∠MON的度数，并说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

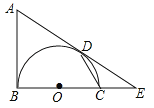
    【题目】（2016浙江省丽水市）如图，AB是以BC为直径的半圆O的切线，D为半圆上一点，AD=AB，AD，BC的延长线相交于点E．

    （1）求证：AD是半圆O的切线；

    （2）连结CD，求证：∠A=2∠CDE；

    （3）若∠CDE=27°，OB=2，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形中，是的中点，延长到点，使，连接.

    （1）求证：四边形是平行四边形；

    （2）若，，，求的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）由大小相同的小立方块搭成的几何体如图1，请在图2的方格中画出该几何体的俯视图和左视图．

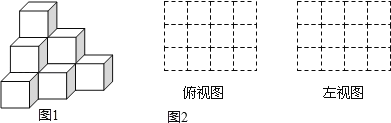
    （2）用小立方体搭一个几何体，使得它的俯视图和左视图与你在方格中所画的一致，则这样的几何体最少要　　　　个小立方块，最多要　　　　个小立方块．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题：探究函数的图象与性质.

    小明根据学习函数的经验，对函数的图象与性质进行了研究.

    下面是小明的研究过程，请补充完成.

    （1）自变量的取值范围是全体实数，与的几组对应值列表如下：

    …

    -4

    -3

    -2

    -1

    0

    4

    …

    …

    2

    1

    0

    n

    0

    1

    m

    3

    4

    …

    其中，m= n= ；

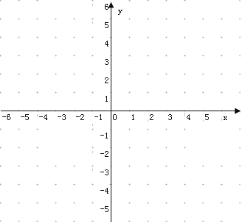
    （2）在如图所示的平面直角坐标中，描出以上表中各对对应值为坐标的点，并根据描出的点，画出该函数的图象.

    （3）观察图象，写出该函数的两条性质.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C，灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行，上午10：00在A处测得灯塔C位于轮船的北偏西30°方向，上午10：40在B处测得灯塔C位于轮船的北偏东60°方向，且与灯塔C相距12km.

    (1)若轮船照此速度与航向航向，何时到达海岸线？

    (2)若轮船不改变航向，该轮船能否停靠在码头？请说明理由(参考数据： ≈1.4， ≈1.7)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

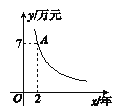
    【题目】朱先生利用分期付款的形式购买了一套住房，他购买的住房的价格为24万元，交了首付之后每年付款y万元，x年结清余款，y与x的函数关系如图所示，请根据图象所提供的信息，回答下列问题：

    （1）确定y与x的函数解析式，并求出首付款的数目；

    （2）朱先生若用10年结清余款，则每年应付多少钱？

    （3）如果朱先生打算每年付款不超过7000元，那么他至少需要几年才能结清余款？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以下说法合理的是（　　）

    A. 小明做了3次掷图钉的实验，发现2次钉尖朝上，由此他说钉尖朝上的概率是

    B. 某彩票的中奖概率是5%，那么买100张彩票一定有5张中奖

    C. 某射击运动员射击一次只有两种可能的结果：中靶与不中靶，所以他击中靶的概率是

    D. 小明做了3次掷均匀硬币的实验，其中有一次正面朝上，2次正面朝下，他认为再掷一次，正面朝上的概率还是

    查看答案和解析>>

    同步练习册答案