
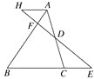
【题目】如图,△ABC中,D是AC的中点,E是BC延长线上一点,过A作AH∥BE,连接ED并延长交AB于F,交AH于H.
(1)求证:AH=CE;
(2)如果AB=4AF,EH=8,求DF的长.
【答案】(1)见解析;(2)2.
【解析】
(1)由于点D是AC的中点,AH∥CE,由平行线的性质知,可推出△ADH≌△CDE,故可得AH=CE;
(2)由平行线分对应线段成比例的性质知,AF∶AB=HF∶HE=1∶4,求得HF的值,由AH∥BE,D是AC的中点可得,点D也是EH的中点,求得HD的值,故有FD=HD-HF.
(1)证明 ∵AH∥BE,D是AC的中点,
∴△ADH≌△CDE,
∴AH=CE.
(2)解 ∵AB=4AF,AH∥BE,
∴AF∶AB=HF∶HE=1∶4,
∴HF=![]() EH=2,
EH=2,
∵AH∥BE,D是AC的中点,
∴点D也是EH的中点,即HD=![]() EH=4,
EH=4,
∴FD=HD-HF=2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是( )
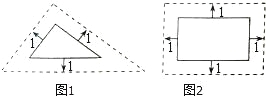
A.甲对,乙不对 B.甲不对,乙对 C.两人都对 D.两人都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个圆形喷水池的中央垂直于水面安装了一个柱形喷水装置OA,O恰好在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,按如图所示建立直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式可以用y=﹣x2+bx+c表示,且抛物线经过点B(![]() ,2),C(2,
,2),C(2,![]() ).请根据以上信息,解答下列问题;
).请根据以上信息,解答下列问题;
(1)求抛物线的函数关系式,并确定喷水装置OA的高度;
(2)喷出的水流距水面的最大高度是多少米?
(3)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?

查看答案和解析>>
科目:初中数学 来源: 题型:
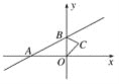
【题目】如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1∶3,则点B的对应点B′的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:选用同一长度单位量得两条线段![]() 、
、![]() 的长度分别是
的长度分别是![]() ,
,![]() ,那么就说两条线段的比
,那么就说两条线段的比![]() :
:
![]() ,如果把
,如果把![]() 表示成比值
表示成比值![]() ,那么
,那么![]() ,或
,或![]() .请完成以下问题:
.请完成以下问题:
![]() 四条线段
四条线段![]() ,
,![]() ,
,![]() ,
,![]() 中,如果________,那么这四条线段
中,如果________,那么这四条线段![]() ,
,![]() ,
,![]() ,
,![]() 叫做成比例线段.
叫做成比例线段.
![]() 已知
已知![]() ,那么
,那么![]() ________,
________,![]() ________
________
![]() 如果
如果![]() ,那么
,那么![]() 成立吗?请用两种方法说明其中的理由.
成立吗?请用两种方法说明其中的理由.
![]() 如果
如果![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则![]() 的值为( )
的值为( )
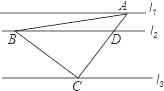
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,给定锐角三角形ABC,小明希望画正方形DEFG,使D,E位于边BC上,F,G分别位于边AC,AB上,他发现直接画图比较困难,于是他先画了一个正方形HIJK,使得点H,I位于射线BC上,K位于射线BA上,而不需要求J必须位于AC上.这时他发现可以将正方形HIJK通过放大或缩小得到满足要求的正方形DEFG.
阅读以上材料,回答小明接下来研究的以下问题:
(1)如图2,给定锐角三角形ABC,画出所有长宽比为2:1的长方形DEFG,使D,E位于边BC上,F,G分别位于边AC,AB上.
(2)已知三角形ABC的面积为36,BC=12,在第(1)问的条件下,求长方形DEFG的面积.
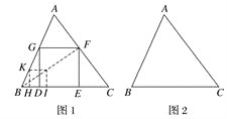
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2,3,根据图中数据完成填空,再按要求答题:sin2A1+sin2B1=____;sin2A2+sin2B2=____;sin2A3+sin2B3=____.
(1)观察上述等式,猜想:在Rt△ABC中,∠C=90°,都有sin2A+sin2B=____;
(2)如图4,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,利用三角函数的定义和勾股定理证明你的猜想;
(3)已知∠A+∠B=90°,且sinA=![]() ,求sinB的值.
,求sinB的值.
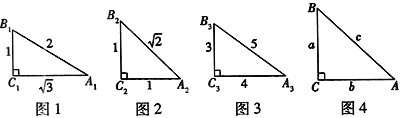
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD的对角线交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
(1)求证:△BDE是直角三角形;
(2)如果OE⊥CD,试判断△BDE与△DCE是否相似,并说明理由.
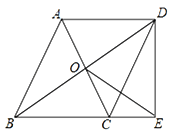
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com