
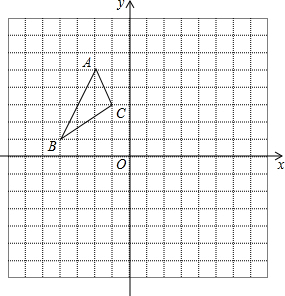
 如图,在平面直角坐标系中,△ABC的位置如图所示.
如图,在平面直角坐标系中,△ABC的位置如图所示.分析 (1)利用点平移的规律写出点A、B、C平移后的对应点A1、B1、C1的坐标,然后描点即可得到△A1B1C1;
(2)根据点平移的规律得到a+3+2=2a,4-b-5=b-3,然后解两个方程即可得到a和b的值;
(3)利用网格特点和旋转的性质画出点A、B、C平移后的对应点A2、B2、C2的坐标,从而得到△A2B2C2.
解答 解:(1)如图,△A1B1C1为所作;
(2)根据题意得a+3+2=2a,4-b-5=b-3,
解得a=5,b=1;
故答案为5,1;
(3)如图,△A2B2C2为所作.
点评 本题考查了旋转作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.


科目:初中数学 来源: 题型:解答题
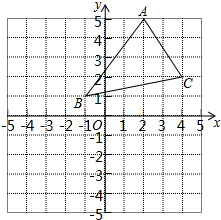 如图,在平面直角坐标系中,三角形ABC的三个顶点A、B、C的坐标分别为(-1,1),(4,2),(2,5),将三角形ABC向左平移3个单位长度,再向下平移5个单位长度.
如图,在平面直角坐标系中,三角形ABC的三个顶点A、B、C的坐标分别为(-1,1),(4,2),(2,5),将三角形ABC向左平移3个单位长度,再向下平移5个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
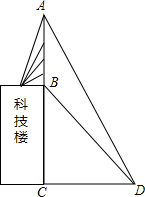 联通公司将移动信号收发塔建在某学校的科技楼上,李明同学利用测倾器在距离科技楼靠塔的一面25米处测得塔顶A的仰角为60°塔底B的仰角为30°,你能利用这些数据帮李明同学计算出该塔的高度吗?($\sqrt{3}$≈1.73,结果精确到0.1米)
联通公司将移动信号收发塔建在某学校的科技楼上,李明同学利用测倾器在距离科技楼靠塔的一面25米处测得塔顶A的仰角为60°塔底B的仰角为30°,你能利用这些数据帮李明同学计算出该塔的高度吗?($\sqrt{3}$≈1.73,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com