
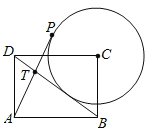
【题目】如图,在矩形ABCD中,AB=3,![]() ,以点C为圆心作⊙O与直线BD相切,点P是⊙O上的一个动点,连接AP交BD于点T,则
,以点C为圆心作⊙O与直线BD相切,点P是⊙O上的一个动点,连接AP交BD于点T,则![]() 的最大值是( )
的最大值是( )
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
【答案】D
【解析】
如图,过点A作AG⊥BD于G点,利用矩形的性质结合勾股定理求出BD,由此提高等面积法求得![]() ,从而得分析出圆的半径为
,从而得分析出圆的半径为![]() ,紧接着过点P作PE⊥BD于点E,提高证明
,紧接着过点P作PE⊥BD于点E,提高证明![]() 利用相似三角形性质得出
利用相似三角形性质得出![]() ,据此根据题意分析出要使
,据此根据题意分析出要使![]() 最大,则
最大,则![]() 最大,即PE最大,最后进一步分析求解即可.
最大,即PE最大,最后进一步分析求解即可.
如图,过点A作AG⊥BD于G点,
∵∠BAD=90°,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴点C到BD的距离为![]() ,
,
∵BD是圆的切线,
∴圆的半径为![]() ,
,
过点P作PE⊥BD于点E,
∴∠AGT=∠PET,
∵∠ATG=∠PTE,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
要使![]() 最大,则
最大,则![]() 最大,即PE最大,
最大,即PE最大,
∵点P是圆上动点,BD是圆的切线,
∴PE最大为圆的直径,
即PE最大值为:3,
∴![]() 最大值为
最大值为![]() ,
,
故选:D.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC与BD交于点O,已知AB=OA,按以下步骤作图:①以点A为圆心,以任意长为半径画弧交AB于M,交AC于点N;②分别以点M,N为圆心,以大于![]() MN为半径画弧,两弧相交于点E;③作射线AE交BC于点F,连接DF.若AB=
MN为半径画弧,两弧相交于点E;③作射线AE交BC于点F,连接DF.若AB=![]() ,则线段DF的长为_____.
,则线段DF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一根木棒AB,斜靠在与地面OM垂直的墙壁ON上,当木棒A端沿NO向下滑动时,同时B端沿射线OM向右滑动,实践发现木棒的中点P运动的路径是一个优美的几何图形,我们把这样的点叫优美点.如果木棒AB长为4,与地面的倾斜角∠ABO=60°.
(1)当木棒A端沿NO向下滑动到点O时,同时B端沿射线OM向右滑动到B′时,木棒的中点P所经过的路径长为多少?
(2)若点P为OB上由点O向点B运动的一运动点,连接AP.
①如图2,设AP的中点为G,问点G是不是优美点,如是,请求出点P运动过程中G所经过的路径长.
②如图3,过点B作BR⊥AP,垂足为点R.点P运动过程中,点R是不是优美点,如是,请求出点R所经过的路径长.
(3)如图4,若点P以每秒1个单位长度由点B向点O运动,同时点Q以每秒![]() 个单位长度的速度由点A向点O运动,连接PQ,S为PQ的中点,则在PQ的运动过程中,点S经过的路径长为多少?(直接写结果)
个单位长度的速度由点A向点O运动,连接PQ,S为PQ的中点,则在PQ的运动过程中,点S经过的路径长为多少?(直接写结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
一般地,如果一个数列从第![]() 项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个常数叫做等差数列的公差,它通常用字母
项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个常数叫做等差数列的公差,它通常用字母![]() 表示,我们可以用公式
表示,我们可以用公式![]() 来计算等差数列的和.(公式中的n表示数的个数,a表示第一个数的值,)
来计算等差数列的和.(公式中的n表示数的个数,a表示第一个数的值,)
例如:3+5+7+9+11+13+15+17+19+21=10×3+![]() ×2=120.
×2=120.
用上面的知识解决下列问题.
(1)计算:2+8+14+20+26+32+38+44+50+56+62+68+74+80+86+92+98+104+110+116
(2)某县决定对坡荒地进行退耕还林.从2009年起在坡荒地上植树造林,以后每年植树后坡荒地的实际面积按一定规律减少,下表为2009、2010、2011、2012四年的坡荒地面积的统计数据.问到哪一年,可以将全县所有坡荒地全部种上树木.
2009年 | 2010年 | 2011年 | 2012年 | |
植树后坡荒地的实际面积(公顷) | 25 200 | 24 000 | 22 400 | 20400 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学生课外阅读,开阔视野,某校开展了“书香校园,诵读经典”活动,学校随机抽查了部分学生,对他们每天的课外阅读时间进行调查,并将调查统计的结果分为四类:每天诵读时间![]() 分钟的学生记为
分钟的学生记为![]() 类,20分钟
类,20分钟![]() 分钟记为
分钟记为![]() 类,40分钟
类,40分钟![]() 分钟记为
分钟记为![]() 类,
类,![]() 分钟记为
分钟记为![]() 类,收集的数据绘制如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
类,收集的数据绘制如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
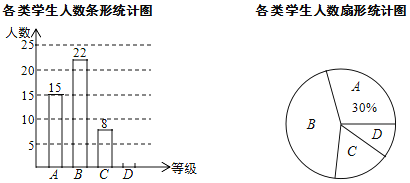
(1)这次共抽取了__________名学生进行调查统计,扇形统计图中![]() 类所对应的扇形圆心角大小为___________;
类所对应的扇形圆心角大小为___________;
(2)将条形统计图补充完整;
(3)如果该校共有2000名学生,请你估计该校![]() 类学生约有多少人?
类学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. “打开电视,正在播放新闻节目”是必然事件
B. “抛一枚硬币,正面进上的概率为![]() ”表示每抛两次就有一次正面朝上
”表示每抛两次就有一次正面朝上
C. “抛一枚均匀的正方体骰子,朝上的点数是6的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的频率稳定在![]() 附近
附近
D. 为了解某种节能灯的使用寿命,选择全面调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.
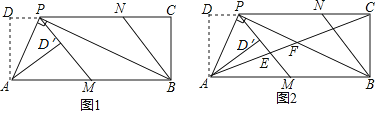
(1)求证:AD2=DPPC;
(2)请判断四边形PMBN的形状,并说明理由;
(3)如图2,连接AC,分别交PM,PB于点E,F.若![]() =
=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com