
分析 (1)利用勾股定理计算出AB长,再根据平行四边形的性质可得CD=AB=10;
(2)①CD是平行四边形的一条边,那么有AB=CD;②CD是平行四边形的一条对角线,过C作CM⊥AO于M,过D作DF⊥AO于F,交AC于Q,过B作BN⊥DF于N,证△DBN≌△CAM,推出DN=CM=a,BN=AM=8-a,得出D((8-a,6+a),由勾股定理得:CD2=(8-a-a)2+(6+a+a)2=8a2-8a+100=8(a-$\frac{1}{2}$)2+98,求出即可.
解答 解:(1)∵A(8,0),B(0,6),
∴AB=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∵CD为平行四边形ABCD边,
∴CD=AB=10,
故答案为:10;
(2)有两种情况:
①CD是平行四边形的一条边,那么有AB=CD=10
②CD是平行四边形的一条对角线,
过C作CM⊥AO于M,过D作DF⊥AO于F,交AC于Q,过B作BN⊥DF于N,
则∠BND=∠DFA═∠CMA=∠QFA=90°,
∠CAM+∠FQA=90°,∠BDN+∠DBN=90°,
∵四边形ACBD是平行四边形,
∴BD=AC,∠C=∠D,BD∥AC,
∴∠BDF=∠FQA,
∴∠DBN=∠CAM,
在△DBN和△CAM中,
$\left\{\begin{array}{l}{∠BND=∠AMC}\\{∠DBN=∠CAM}\\{BD=AC}\end{array}\right.$,
∴△DBN≌△CAM(AAS),
∴DN=CM=a,BN=AM=8-a,
D((8-a,6+a),
由勾股定理得:CD2=(8-a-a)2+(6+a+a)2=8a2-8a+100=8(a-$\frac{1}{2}$)2+98,
当a=$\frac{1}{2}$时,CD有最小值,是$\sqrt{98}$,∵$\sqrt{98}$<10,
∴CD的最小值是$\sqrt{98}$=7$\sqrt{2}$.
故答案为:7$\sqrt{2}$.
点评 本题考查了平行四边形性质,全等三角形的性质和判定,二次函数的最值的应用,关键是能得出关于a的二次函数解析式,题目比较好,难度偏大.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:选择题
| A. | 有且只有一条直线与已知直线平行 | |
| B. | 垂直于同一条直线的两条直线互相平行 | |
| C. | 从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离 | |
| D. | 在平面内过一点有且只有一条直线与已知直线垂直 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
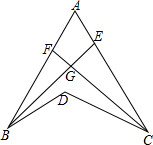 如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,则∠A为( )
如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,则∠A为( )| A. | 70° | B. | 75° | C. | 80° | D. | 85° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | S和p | B. | S和a | C. | p和a | D. | S,p,a |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点D在线段BC上,已知∠BAC=90°,∠DAC+∠C=90°,则∠BAD和∠C的大小关系是∠BAD=∠C,其依据是同角的余角相等.
如图,点D在线段BC上,已知∠BAC=90°,∠DAC+∠C=90°,则∠BAD和∠C的大小关系是∠BAD=∠C,其依据是同角的余角相等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com