

分析 (1)由AB=AC,∠BPC=60°,易得△ABC为等边三角形,又由∠ACB的平分线交⊙O于点P,可得∠BCP=30°,即可得∠PBC=90°,证得CP为⊙O的直径;
(2)首先过点E作EG⊥AC于G,连接OB,OC,易证得∠ACP=∠PCB,即可得sin∠FOC=sin∠BPC=$\frac{24}{25}$,然后设FC=24a,则OC=OA=25a,由勾股定理,可求得a的值,然后由在Rt△AGE和Rt△AFC中,EG=EF,FC=24,AF=32,AC=40,sin∠FAC=$\frac{EG}{AE}$=$\frac{FC}{AC}$,求得答案.
解答 解:(1)∵∠BPC=60°,
∴∠BAC=∠BPC=60°.
又∵AB=AC,
∴△ABC为等边三角形,
∴∠ACB=60°,
∵∠ACB的平分线交⊙O于点P,
∴∠BCP=30°,
∴∠PBC=180°-∠BPC-∠BCP=90°,
∴CP为⊙O的直径.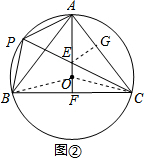 (2)过点E作EG⊥AC于G,连接OB,OC.
(2)过点E作EG⊥AC于G,连接OB,OC.
∵AB=AC,AF所在的直线为⊙O的对称轴,
∴AF⊥BC,BF=CF.
∵∠ACP=∠PCB,
∴EG=EF,
∵∠BPC=$\frac{1}{2}$∠BOC=∠FOC,
∴sin∠FOC=sin∠BPC=$\frac{24}{25}$,
设FC=24a,则OC=OA=25a,
由勾股定理可得OF=7a,
∴AF=25a+7a=32a,
在Rt△AFC中,AC=$\sqrt{A{F}^{2}+F{C}^{2}}$=40a,
又∵AB=AC=40,
∴40a=40,
∴a=1,
∴FC=24,AF=32
在Rt△AGE和Rt△AFC中,
EG=EF,FC=24,AF=32,AC=40,sin∠FAC=$\frac{EG}{AE}$=$\frac{FC}{AC}$,
即$\frac{EF}{32-EF}$=$\frac{24}{40}$,解得EF=12.
点评 此题考查了圆的外接圆的性质、圆周角定理、等边三角形的判定与性质、勾股定理以及三角函数等知识.注意准确作出辅助线是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.5cm | B. | 1cm | C. | 2cm | D. | 3cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 球类 | 进价(元/个) | 标价(元/个) |
| 篮球 | 70 | 90 |
| 排球 | 50 | 65 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | -8 | C. | $-\frac{1}{8}$ | D. | $-\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com