
【题目】如图,一次函数y=kx+b的图象与反比例函数 ![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积.
【答案】
(1)解:∵点A(﹣2,1)在反比例函数 ![]() 的图象上,
的图象上,
∴m=(﹣2)×1=﹣2.
∴反比例函数的表达式为 ![]() .
.
∵点B(1,n)也在反比例函数 ![]() 的图象上,
的图象上,
∴n=﹣2,即B(1,﹣2).
把点A(﹣2,1),点B(1,﹣2)代入一次函数y=kx+b中,
得 ![]() 解得
解得 ![]() .
.
∴一次函数的表达式为y=﹣x﹣1
(2)解:∵在y=﹣x﹣1中,当y=0时,得x=﹣1.
∴直线y=﹣x﹣1与x轴的交点为C(﹣1,0).
∵线段OC将△AOB分成△AOC和△BOC,
∴S△AOB=S△AOC+S△BOC= ![]() ×1×1+
×1×1+ ![]() ×1×2=
×1×2= ![]() +1=
+1= ![]() .
.
【解析】(1)由A在反比例函数图象上可求得k的值,再由B在反比例函数图象上可求得n的值,再由待定系数法求得一次函数的表达式;
(2)由一次函数的表达式y=-x-1求出直线y=﹣x﹣1与x轴、y轴的交点坐标,再由S△AOB=S△AOC+S△BOC可求出答案.
【考点精析】本题主要考查了确定一次函数的表达式的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:初中数学 来源: 题型:
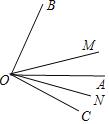
【题目】如图,已知OM、OA、ON是∠BOC内的三条射线,ON平分∠AOC,OM平分∠BOC,且∠AOB+∠MON=120°,则∠MON=______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
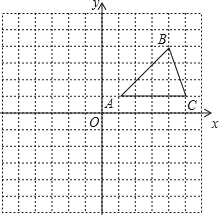
【题目】在平面直角坐标系中,△ABC的位置如图所示,(每个小方格都是边长为1个单位长度的正方形).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转180°,画出旋转后得到的△A2B2C2,并直接写出点B2,C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线l与x轴、y轴分别交于点B(4,0)、C(0,3),点A为x轴负半轴上一点,AM⊥BC于点M交y轴于点N(0, ![]() ).已知抛物线y=ax2+bx+c经过点A,B,C.
).已知抛物线y=ax2+bx+c经过点A,B,C.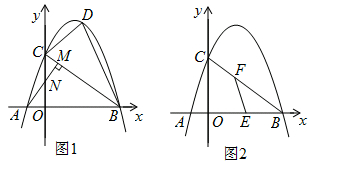
(1)求抛物线的函数式.
(2)连接AC,点D在线段BC上方的抛物线上,连接DC,DB,若△BCD和△ABC面积满足S△BCD= ![]() S△ABC , 求点D的坐标.
S△ABC , 求点D的坐标.
(3)如图2,E为OB中点,设F为线段BC上一点(不含端点),连接EF.一动点P从E出发,沿线段EF以每秒3个单位的速度运动到F,再沿着线段PC以每秒5个单位的速度运动到C后停止.若点P在整个运动过程中用时最少,请直接写出最少时间和此时点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=( )

A. 40°B. 45°C. 50°D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,高新区凌水河治理工程正式启动,若由甲工程队单独完成需10个月;若由甲、乙两工程队合做4个月后,剩下工程由乙工程队再做5个月可以完成。(1)乙工程队单独完成这项工程需几个月的时间?
(2)已知甲工程队每月施工费用为15万元,比乙工程队多6万元,按要求该工程总费用不超过141万元,工程必须在一年内竣工(包括12个月).为了确保经费和工期,采取甲、乙工程队同时开工,甲工程队做![]() 个月,乙工程队做
个月,乙工程队做![]() 个月(
个月(![]() 均为整数)分工合作的方式施工,问有哪几种施工方案?
均为整数)分工合作的方式施工,问有哪几种施工方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们知道:“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.”
(1)请写出它的逆命题 ;该逆命题是一个 命题(填“真”或“假”)
(2)若你的判断是真命题请写出证明过程(要求画图,并写出已知,求证).若是假命题,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com