
(1)阅读理解:
我们知道,只用直尺和圆规不能解决的三个经典的希腊问 题之一是三等分任意角,但是这个任务可以借助如图所示的一边上有刻度的勾尺完成,勾尺的直角顶点为P,“宽臂”的宽度=PQ=QR=RS,(这个条件很重要哦!)勾尺的一边MN满足M,N,Q三点共线(所以PQ⊥MN).
题之一是三等分任意角,但是这个任务可以借助如图所示的一边上有刻度的勾尺完成,勾尺的直角顶点为P,“宽臂”的宽度=PQ=QR=RS,(这个条件很重要哦!)勾尺的一边MN满足M,N,Q三点共线(所以PQ⊥MN).
下面以三等分∠ABC为例说明利 用勾尺三等分锐角的过程:
用勾尺三等分锐角的过程:
第一步:画直线DE使DE//BC,且这两条平行线的距离等于PQ;
第二步:移动勾尺到合适位置,使其顶点P落在DE上,使勾尺的MN边经过点B, 同时让点R落在∠ABC的BA边上;
同时让点R落在∠ABC的BA边上;
第三步:标记此 时点Q和点P所在位置,作射线BQ和射线BP.
时点Q和点P所在位置,作射线BQ和射线BP.
请完成第三步操作,图中的三等分线是射线____、____.
(2)在(1)的条件下完成三等分∠ABC的证明过程:
(3 )在(1)的条件下探究:
)在(1)的条件下探究:
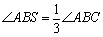 是否成立?如果成立,请说明理由;如
是否成立?如果成立,请说明理由;如 果不成立,请在下图中
果不成立,请在下图中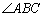 的外部画出
的外部画出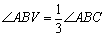 (无需写画法,保留画
(无需写画法,保留画 图痕迹即可).
图痕迹即可).

科目:初中数学 来源: 题型:
植树 节前夕,某林场组织20辆汽车装运芒果树、木棉树和垂叶榕三种树木共100棵来深圳销售.按计划20辆车都要装运,每辆汽车只能装运同一种树木,且必须装满.根据表格提供的信息,解答下列问题.
节前夕,某林场组织20辆汽车装运芒果树、木棉树和垂叶榕三种树木共100棵来深圳销售.按计划20辆车都要装运,每辆汽车只能装运同一种树木,且必须装满.根据表格提供的信息,解答下列问题.
(1)设装运芒果树的车辆数为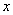 ,装运木棉树的车辆数为
,装运木棉树的车辆数为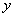 ,求
,求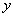 与
与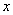 之间的函数关系式;(3分)
之间的函数关系式;(3分)
(2)如果安排装运芒果树的车辆数不少于5辆,装运木棉树的车辆数不少于6辆,那么车辆的安排有几种方案?并写出每种安排方案?(3分)
(3)若要求总运费最少,应采用(2)中哪种安排方案?并求出最少总运费?(3分)
| 树木种类 | 芒果树 | 木棉树 | 垂叶榕 |
| 每辆汽车运载量(棵) | 6 | 5 | 4 |
| 平均每棵树运费(元) | 120 | 160 | 180 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图, 在△ABC中,AB=AC,∠BAC=30°.点D为△ABC内一点,且DB=DC,∠DCB=30°.点E为BD
在△ABC中,AB=AC,∠BAC=30°.点D为△ABC内一点,且DB=DC,∠DCB=30°.点E为BD 延长线上一
延长线上一 点,且A
点,且A E=AB.
E=AB.
(1)求∠ADE的度数;
(2)若点M在DE上,且DM=D
 A,求证:ME=DC.
A,求证:ME=DC.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)求证:△ODE是等边三角形.
 (2)线段BD、DE、EC 三者有什么数量关系?写出你的判断过程.
(2)线段BD、DE、EC 三者有什么数量关系?写出你的判断过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
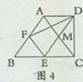
如图4,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F,E分别是AB,BC的中点,则下列结论不一定正确的是( )
A.△ABC是等腰三角形 B.四边形EFAM是菱形
C.S△BEF=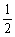 S△ACD D.DE平分∠CDF
S△ACD D.DE平分∠CDF
查看答案和解析>>
科目:初中数学 来源: 题型:
一项工程要在限期内完成,如果第一组单独做,恰好按规定日期完成;如果第二组单独
做,需要超过规定日期4天才能完成,如果两组合作3天后,剩下的工程由第二组单独
做,正好在规定日期内完成,问规定日期是多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com