
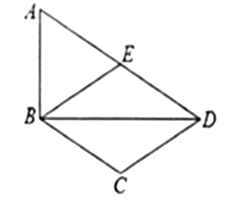
【题目】如图,在四边形ABCD中,BD为一条对角线,![]() 且
且![]() ,
,![]() ,E为AD的中点,连接BE.
,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分![]() ,
,![]() ,求AC的长.
,求AC的长.
【答案】(1)详见解析(2)![]()
【解析】
(1) 题干中由![]() 且
且![]() 可知,一组对边平行且相等的四边形是平行四边形,则四边形BCDE是平行四边形,又知BE是直角三角形斜边的中线,直角三角形斜边的中线等于斜边的一半,则得到BE=ED,从而再用一组邻边相等的平行四边形是菱形证明即可.
可知,一组对边平行且相等的四边形是平行四边形,则四边形BCDE是平行四边形,又知BE是直角三角形斜边的中线,直角三角形斜边的中线等于斜边的一半,则得到BE=ED,从而再用一组邻边相等的平行四边形是菱形证明即可.
(2)通过 DE∥BC和 AC平分![]() ,可得到∠BAC=∠ACB,从而由等角对等边得到AB=BC=1,则此时直角三角形ABD,有一个执教不是斜边的一半,则可知这个直角边对应的角是30°,找到30°才是题目的突破口,然后依次得到角度的关系,证明得到三角形ACD是直角三角形,再用勾股定理解得AC的长.
,可得到∠BAC=∠ACB,从而由等角对等边得到AB=BC=1,则此时直角三角形ABD,有一个执教不是斜边的一半,则可知这个直角边对应的角是30°,找到30°才是题目的突破口,然后依次得到角度的关系,证明得到三角形ACD是直角三角形,再用勾股定理解得AC的长.
(1)证明:∵DE∥BC且DE=BC(已知)
∴四边形BCDE是平行四边形(一组对边平行且相等的四边形是平行四边形)
又∵E为直角三角形斜边AD边的中点(已知)
∴BE=![]() AD,即BE=DE(直角三角形斜边的中线等于斜边的一半)
AD,即BE=DE(直角三角形斜边的中线等于斜边的一半)
∴平行四边形四边形BCDE是菱形(一组邻边相等的平行四边形是菱形)
(2)
连接AC,如图可知:
∵DE∥BC(已知)
∴∠DAC=∠ACB(两直线平行内错角相等)
又∵AC平分![]() (已知)
(已知)
∴∠BAC=∠DAC(角平分线的定义)
即∠BAC=∠ACB(等量代换)
∴AB=BC=1(等角对等边)
由(1)可知:AD=2ED=2BC=2
在直角三角形中AB=1,AD=2
∴∠ADB=30°(直角三角形中,若一个直角边是斜边 一半,则这个直角边所对的角是30°)
∴∠BAD=60°(直角三角形两锐角互余)
即∠CAD=![]() ∠BAD=30°(角平分线的定义),∠ADC=2∠ADB=60°(菱形的性质)
∠BAD=30°(角平分线的定义),∠ADC=2∠ADB=60°(菱形的性质)
所以三角形ADC是直角三角形.
则由![]() 可知:
可知:
![]()


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】已知A,B,C三点共线,线段AB=20 cm,BC=8 cm,点E,F分别是线段AB,BC的中点,则线段EF的长为( )
A.28 cm或12 cmB.28 cmC.14 cmD.14cm或6 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象经过点
的图象经过点![]() ,
,![]() ,点A关于抛物线对称轴的对称点为点C,点P是抛物线对称轴右侧图象上的一点,点
,点A关于抛物线对称轴的对称点为点C,点P是抛物线对称轴右侧图象上的一点,点![]() .
.
![]() 求出点C坐标及抛物线的解析式;
求出点C坐标及抛物线的解析式;
![]() 若以A,C,P,G为顶点的四边形面积等于30时,求点P的坐标;
若以A,C,P,G为顶点的四边形面积等于30时,求点P的坐标;
![]() 若Q为线段AC上一动点,过点Q平行于y轴的直线与过点G平行于x轴的直线交于点M,将
若Q为线段AC上一动点,过点Q平行于y轴的直线与过点G平行于x轴的直线交于点M,将![]() 沿QG翻折得到
沿QG翻折得到![]() ,当点N在坐标轴上时,求Q点的坐标.
,当点N在坐标轴上时,求Q点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进“足球进校园”活动的开展,某市举行了中学生足球比赛活动现从A,B,C三支获胜足球队中,随机抽取两支球队分别到两所边远地区学校进行交流.
(1)请用列表或画树状图的方法(只选择其中一种),表示出抽到的两支球队的所有可能结果;
(2)求出抽到B队和C队参加交流活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
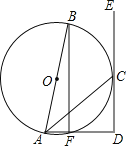
【题目】如图,AB是⊙O的直径,ED切⊙O于点C,AD交⊙O于点F,∠AC平分∠BAD,连接BF.
(1)求证:AD⊥ED;
(2)若CD=4,AF=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在长方形ABCD中,AB=5,第一次平移将长方形ABCD沿AB方向向右平移4个单位长度,得到长方形A1B1C1D1,第二次平移将长方形A1B1C1D1沿A1B1方向向右平移4个单位长度,得到长方形A2B2C2D2,……,第n次平移将长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1方向向右平移4个单位长度,得到长方形AnBnCnDn(n>2).若ABn的长为45,则n=( )
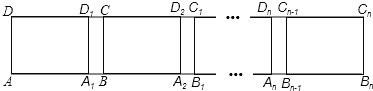
A.10B.11C.16D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,AM的延长线交BC于点N,连接DM,下列结论:①AE=AF;②DF=DN;③AN=BF;④EN⊥NC;⑤AE=NC,其中正确结论的个数是( )
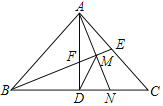
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一组数据x1,x2,x3,x4,…xn,的方差为5,则另一组数据2x1+3,2x2+3,2x3+3,2x4+3,…2xn+3的方差为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
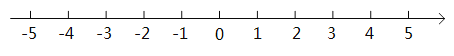
(1)探究:
①数轴上表示![]() 和
和![]() 的两点之间的距离是 ;
的两点之间的距离是 ;
②数轴上表示![]() 和
和![]() 的两点之间的距离是 ;
的两点之间的距离是 ;
③数轴上表示![]() 和
和![]() 的两点之间的距离是 ;
的两点之间的距离是 ;
(2)归纳:
一般的,数轴上表示数m与数n的两点之间的距离等于 .
(3)应用:
①如果表示数![]() 和3的两点之间的距离是9,则可记为:
和3的两点之间的距离是9,则可记为:![]() ,那么
,那么![]() .
.
②若数轴上表示数![]() 的点位于
的点位于![]() 与
与![]() 之间,求
之间,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com