
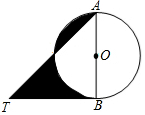
 如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )
如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )| A. | 2 | B. | $\frac{3}{2}$-$\frac{1}{4}$π | C. | 1 | D. | $\frac{1}{2}$+$\frac{1}{4}$π |
分析 设AT交⊙O于D,连结BD,先根据圆周角定理得到∠ADB=90°,则可判断△ADB、△BDT都是等腰直角三角形,所以AD=BD=TD=$\frac{\sqrt{2}}{2}$AB=$\sqrt{2}$,然后利用弓形AD的面积等于弓形BD的面积得到阴影部分的面积=S△BTD.
解答  解:∵BT是⊙O的切线;
解:∵BT是⊙O的切线;
设AT交⊙O于D,连结BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
而∠ATB=45°,
∴△ADB、△BDT都是等腰直角三角形,
∴AD=BD=TD=$\frac{\sqrt{2}}{2}$AB=$\sqrt{2}$,
∴弓形AD的面积等于弓形BD的面积,
∴阴影部分的面积=S△BTD=$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{2}$=1.
故选C.
点评 本题考查了切线的性质,等腰直角三角形的性质,解决本题的关键是利用等腰直角三角形的性质把阴影部分的面积转化为三角形的面积.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 矩形的对角线相互垂直 | |
| B. | 顺次连结对角线相等的四边形各边中点所得到的四边形是矩形 | |
| C. | 等边三角形既是轴对称图形又是中心对称图形 | |
| D. | 对角线互相垂直平分的四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (120-30$\sqrt{5}$)cm | B. | (160-60$\sqrt{5}$)cm | C. | (60$\sqrt{5}$-120)cm | D. | (60$\sqrt{5}$-6)cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
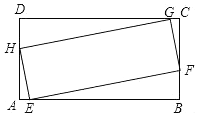 如图,四边形EFGH与四边形ABCD均为矩形,点E,F,G,H分别在边AB,BC,CD,DA上,且EF=3HE,AB=2BC,则tan∠AHE=( )
如图,四边形EFGH与四边形ABCD均为矩形,点E,F,G,H分别在边AB,BC,CD,DA上,且EF=3HE,AB=2BC,则tan∠AHE=( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{7}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 红红不是胜就是输,所以红红胜的概率为$\frac{1}{2}$ | |
| B. | 红红胜或娜娜胜的概率相等 | |
| C. | 两人出相同手势的概率为$\frac{1}{3}$ | |
| D. | 娜娜胜的概率和两人出相同手势的概率一样 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
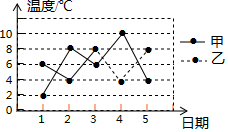 甲、乙两地去年12月前5天的日平均气温如图所示,下列描述错误的是( )
甲、乙两地去年12月前5天的日平均气温如图所示,下列描述错误的是( )| A. | 两地气温的平均数相同 | B. | 甲地气温的中位数是6℃ | ||
| C. | 乙地气温的众数是4℃ | D. | 乙地气温相对比较稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法判断 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com