
| S△DAC+S△DBC | 2 |
| 1 |
| 2 |
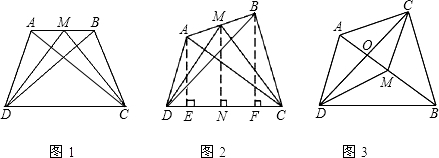
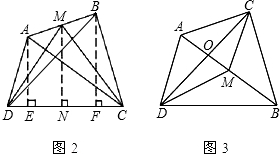 解:(1)当AB和CD不平行时,结论①仍然成立.
解:(1)当AB和CD不平行时,结论①仍然成立.| 1 |
| 2 |
| 1 |
| 2 |
| S△DAC+S△DBC |
| 2 |
| S△DBC-S△DAC |
| 2 |


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
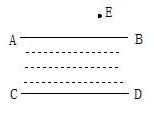 13、如图,直线AB,CD是一条河的两岸,并且AB∥CD,点E为直线AB,CD外的一点,为了过E作河岸CD的平行线,只需作岸AB的平行线即可,其理由是
13、如图,直线AB,CD是一条河的两岸,并且AB∥CD,点E为直线AB,CD外的一点,为了过E作河岸CD的平行线,只需作岸AB的平行线即可,其理由是查看答案和解析>>
科目:初中数学 来源: 题型:
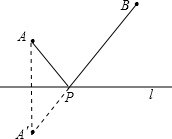 几何模型:
几何模型:| 5 |
| 5 |
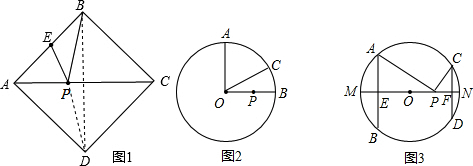
查看答案和解析>>
科目:初中数学 来源:2001年全国中考数学试题汇编《四边形》(03)(解析版) 题型:解答题
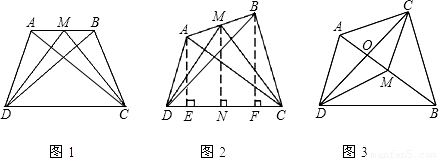
 .
.
查看答案和解析>>
科目:初中数学 来源:2001年安徽省中考数学试卷(解析版) 题型:解答题
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com